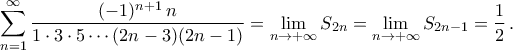Υπολογισμός σειράς
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Υπολογισμός σειράς
Γρηγόρη,
το αποτέλεσμα περιέχει τη συνάρτηση erfi ; Διότι αυτή βγάζω.
Σημείωση: Κρίμα, και νόμισα θα πέσω πάνω στα Catalan.
Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Υπολογισμός σειράς
Υπόδειξη: Η απάντηση είναιTolaso J Kos έγραψε: ↑Τρί Μάιος 08, 2018 11:30 pmτο αποτέλεσμα περιέχει τη συνάρτηση erfi ; Διότι αυτή βγάζω.
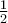
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Υπολογισμός σειράς
Ισχύει

Αν με
 συμβολίσουμε τα μερικά αθροίσματα τότε ισχύει
συμβολίσουμε τα μερικά αθροίσματα τότε ισχύει 
 και
και 

Η απόδειξη γίνεται με επαγωγή. Για την
 έχουμε:
έχουμε:Για
 ισχύει αφού
ισχύει αφού 
Αν ισχύει για
 θα δείξουμε ότι ισχύει για
θα δείξουμε ότι ισχύει για  .
.Πράγματι

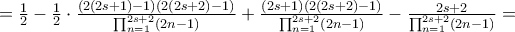

 .
.Όμοια δείχνουμε τη
 .
.Οι
 και
και  αποδεικνύουν ότι η σειρά συγκλίνει στο
αποδεικνύουν ότι η σειρά συγκλίνει στο 
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Υπολογισμός σειράς
Να συμπληρώσω μόνο πως κατέληξα στις σχέσεις 
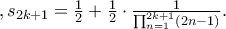
Υπολογίζουμε τα πρώτα μερικά αθροίσματα (δεν χρειάζεται πολλά) από τα οποία παίρνουμε σαν αποτέλεσμα ένα κλάσμα με παρονομαστή το ΕΚΠ των
παρονομαστών που προφανώς είναι το και αριθμητή τον
και αριθμητή τον  παρονομαστή
παρονομαστή  .
.
Μετά γράφουμε και μένει να το αποδείξουμε ότι ισχύει γενικά.
και μένει να το αποδείξουμε ότι ισχύει γενικά.

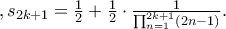
Υπολογίζουμε τα πρώτα μερικά αθροίσματα (δεν χρειάζεται πολλά) από τα οποία παίρνουμε σαν αποτέλεσμα ένα κλάσμα με παρονομαστή το ΕΚΠ των
παρονομαστών που προφανώς είναι το
 και αριθμητή τον
και αριθμητή τον  παρονομαστή
παρονομαστή  .
.Μετά γράφουμε
 και μένει να το αποδείξουμε ότι ισχύει γενικά.
και μένει να το αποδείξουμε ότι ισχύει γενικά.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες