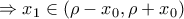Έστω συνάρτηση
![f: [a,b] \to \mathbb{R} f: [a,b] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/4fde3b6222b0a96510fa042105c32213.png) δύο φορές παραγωγίσιμη με
δύο φορές παραγωγίσιμη με  και
και  για κάθε
για κάθε ![x \in [a,b] x \in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/af3c1adca188345d2a91c0d13a891b9f.png) , καθώς επίσης και
, καθώς επίσης και  . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι: 1. Υπάρχει μοναδική ρίζα
 της
της  .
. 2. Yπάρχει υποδιάστημα (θετικού μέτρου)
![I \subseteq [a,b] I \subseteq [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/5ede437891302b2063f8ed74c01f4bf5.png) τέτοιο ώστε, για κάθε
τέτοιο ώστε, για κάθε  , η ακολουθία με αναδρομικό τύπο
, η ακολουθία με αναδρομικό τύπο  συγκλίνει στο
συγκλίνει στο  .
.
![f'(x)\geq M \forall x\in [a,b] f'(x)\geq M \forall x\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/fc5fad089c0c5bdc6b6574b33434a46f.png) ή
ή ![f'(x)\leq -M \forall x\in [a,b] f'(x)\leq -M \forall x\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/605850df4031165eb42bbffcabdc3c82.png)






 και
και 




 και
και 


 τότε
τότε