
Ποιὰ ἀνισότητα πρέπει νὰ ἱκανοποιεῖ τὸ
 , ὥστε ἡ σειρὰ
, ὥστε ἡ σειρὰ  νὰ συγκλίνει;
νὰ συγκλίνει;Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

 , ὥστε ἡ σειρὰ
, ὥστε ἡ σειρὰ  νὰ συγκλίνει;
νὰ συγκλίνει; το οποίο βγάζει ότι για να συγκλίνει η σειρά πρέπει
το οποίο βγάζει ότι για να συγκλίνει η σειρά πρέπει  .
.  .
.
Στηριζόμενοι στοΓ.-Σ. Σμυρλής έγραψε: ↑Παρ Φεβ 09, 2018 11:14 amΠΡΟΒΛΗΜΑ. Δίδεται ἡ ἀναδρομικὴ ἀκολουθία
Ποιὰ ἀνισότητα πρέπει νὰ ἱκανοποιεῖ τὸ, ὥστε ἡ σειρὰ
νὰ συγκλίνει;


 αποκλίνει αφού
αποκλίνει αφού αποκλίνει
αποκλίνει αποκλίνει.
αποκλίνει. συγκλίνει.
συγκλίνει.


 . Ξεκινάμε από το ακόλουθο λήμμα:
. Ξεκινάμε από το ακόλουθο λήμμα: είναι μία ακολουθία για την οποία είναι
είναι μία ακολουθία για την οποία είναι  τότε
τότε  Απόδειξη: Άμεση εφαρμογή του Stolz - Cesaro.
Απόδειξη: Άμεση εφαρμογή του Stolz - Cesaro. είναι φθίνουσα και τείνει στο
είναι φθίνουσα και τείνει στο  . Επιπλέον, επειδή
. Επιπλέον, επειδή συνάγουμε ότι
συνάγουμε ότι  . Και άρα από το λήμμα παίρνουμε ότι
. Και άρα από το λήμμα παίρνουμε ότι  . Συνεπώς
. Συνεπώς  .
. και φυσικά
και φυσικά  . Το τελευταίο επιβεβαιώνει και τη παρατήρηση του Σταύρου ότι η σειρά
. Το τελευταίο επιβεβαιώνει και τη παρατήρηση του Σταύρου ότι η σειρά  αποκλίνει.
αποκλίνει.
 ἀναλυτικὴ σὲ περιοχὴ τοῦ μηδενός, καὶ
ἀναλυτικὴ σὲ περιοχὴ τοῦ μηδενός, καὶ  , ὅπου
, ὅπου  , καὶ
, καὶ
 συγκλίνει ἂν καὶ μόνον ἂν
συγκλίνει ἂν καὶ μόνον ἂν  .
. .
.
Θα αναζητήσουμε
 τέτοιο, ώστε
τέτοιο, ώστε 


![=a_{n}^{k}\left [ \left ( 1-\dfrac{a_{n}^{2}}{3!}+\dfrac{a_{n}^{4}}{5!} +o(a_{n}^{4})\right )^k- 1\right ] =a_{n}^{k}\left [ \left ( 1-\dfrac{a_{n}^{2}}{3!}+\dfrac{a_{n}^{4}}{5!} +o(a_{n}^{4})\right )^k- 1\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/29ef186021727ea5eacbdd8e3050e2bb.png)
![=a_{n}^{k}\left [ -k\dfrac{a_{n}^{2}}{3!}+k\dfrac{a_{n}^{4}}{5!}+\dfrac{k(k-1)}{2}\left (\dfrac{a_{n}^{2}}{3!} \right )^2+o(a_{n}^{4})\right ] =a_{n}^{k}\left [ -k\dfrac{a_{n}^{2}}{3!}+k\dfrac{a_{n}^{4}}{5!}+\dfrac{k(k-1)}{2}\left (\dfrac{a_{n}^{2}}{3!} \right )^2+o(a_{n}^{4})\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b2d5393e470282578dc6b059d69ab7d4.png)

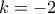 (θεώρησα δεδομένο ότι
(θεώρησα δεδομένο ότι  ) και επομένως
) και επομένως
 παίρνουμε
παίρνουμε






Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 5 επισκέπτες