 , όπου
, όπου  το ακέραιο μέρος, έχει μια υπακολουθία με όλους τους όρους της να είναι περιττοί φυσικοί και μια υπακολουθία με όλους τους όρους της να είναι άρτιοι φυσικοί.
το ακέραιο μέρος, έχει μια υπακολουθία με όλους τους όρους της να είναι περιττοί φυσικοί και μια υπακολουθία με όλους τους όρους της να είναι άρτιοι φυσικοί. ΣΗΜΕΙΩΣΗ: Δεν έχω λύση.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 , όπου
, όπου  το ακέραιο μέρος, έχει μια υπακολουθία με όλους τους όρους της να είναι περιττοί φυσικοί και μια υπακολουθία με όλους τους όρους της να είναι άρτιοι φυσικοί.
το ακέραιο μέρος, έχει μια υπακολουθία με όλους τους όρους της να είναι περιττοί φυσικοί και μια υπακολουθία με όλους τους όρους της να είναι άρτιοι φυσικοί. 
Ευχαριστούμε για την παραπομπή.Γ.-Σ. Σμυρλής έγραψε: ↑Παρ Ιαν 26, 2018 10:36 amΜάλλον ἀποτελεῖ ἀνοικτὸ πρόβλημα:
https://www.researchgate.net/publicatio ... n_modulo_1
 και
και 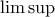 της ακολουθίας
της ακολουθίας  .
. οι "συνήθεις" υπολογιστικές μηχανές μας "εγκαταλείπουν" γρήγορα.
οι "συνήθεις" υπολογιστικές μηχανές μας "εγκαταλείπουν" γρήγορα.
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 21 επισκέπτες