![g:\left [ a, \right b]\rightarrow \mathbb{R} g:\left [ a, \right b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/bcb9e2de6ce00d936e80c21cb92adbee.png) δύο φορές παραγωγίσιμη και γνησίως μονότονη στο
δύο φορές παραγωγίσιμη και γνησίως μονότονη στο ![\left [ a, \right b ] \left [ a, \right b ]](/forum/ext/geomar/texintegr/latexrender/pictures/4b43e9169ec53ac13afe47aea8049dea.png) με
με  . Να δείξετε ότι αν η
. Να δείξετε ότι αν η 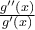 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 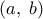 τότε και η
τότε και η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 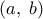 .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![g:\left [ a, \right b]\rightarrow \mathbb{R} g:\left [ a, \right b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/bcb9e2de6ce00d936e80c21cb92adbee.png) δύο φορές παραγωγίσιμη και γνησίως μονότονη στο
δύο φορές παραγωγίσιμη και γνησίως μονότονη στο ![\left [ a, \right b ] \left [ a, \right b ]](/forum/ext/geomar/texintegr/latexrender/pictures/4b43e9169ec53ac13afe47aea8049dea.png) με
με  . Να δείξετε ότι αν η
. Να δείξετε ότι αν η 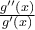 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 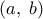 τότε και η
τότε και η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 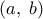 .
. είναι γνησίως αύξουσα. (Σε διαφορετική περίπτωση δουλεύω με την
είναι γνησίως αύξουσα. (Σε διαφορετική περίπτωση δουλεύω με την 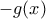 χωρίς να αλλάζει κάτι.)
χωρίς να αλλάζει κάτι.)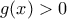 και
και 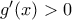 για κάθε
για κάθε ![x \in (a,b] x \in (a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/3e4a5d1c170a3e316025832abad1f084.png) . Έστω
. Έστω  . Από το Θεώρημα Μέσης Τιμής του Cauchy υπάρχει
. Από το Θεώρημα Μέσης Τιμής του Cauchy υπάρχει  ώστε
ώστε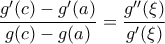
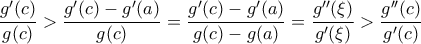
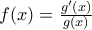 για
για  . Τότε
. Τότε![\displaystyle f'(c) = \frac{g''(c)g(c) - g'(c)^2}{g(c)^2} = \frac{g'(c)}{g(c)}\left[\frac{g''(c)}{g'(c)} - \frac{g'(c)}{g(c)}\right] < 0 \displaystyle f'(c) = \frac{g''(c)g(c) - g'(c)^2}{g(c)^2} = \frac{g'(c)}{g(c)}\left[\frac{g''(c)}{g'(c)} - \frac{g'(c)}{g(c)}\right] < 0](/forum/ext/geomar/texintegr/latexrender/pictures/1ce3b834e732215e8548e35c452ebef4.png)
 είναι γνησίως φθίνουσα όπως θέλαμε να δείξουμε.
είναι γνησίως φθίνουσα όπως θέλαμε να δείξουμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 25 επισκέπτες