Σελίδα 1 από 1
Η αρμονία της Fibonacci
Δημοσιεύτηκε: Σάβ Σεπ 16, 2017 11:06 pm
από Tolaso J Kos
Ας δηλώσουμε με

τον

- οστό όρο Fibonacci και με
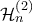
το γενικευμένο αρμονικό όρο τάξης

. Υπολογισθήτω:

Re: Η αρμονία της Fibonacci
Δημοσιεύτηκε: Τετ Σεπ 20, 2017 11:39 pm
από Σεραφείμ
Re: Η αρμονία της Fibonacci
Δημοσιεύτηκε: Πέμ Σεπ 21, 2017 7:52 am
από Tolaso J Kos
Σεραφείμ έγραψε:
Το αποτέλεσμα σίγουρα επιδέχεται οπτική βελτίωση .. αργότερα ...


Κάπως έτσι θαρρώ.

Re: Η αρμονία της Fibonacci
Δημοσιεύτηκε: Πέμ Σεπ 21, 2017 9:06 am
από Tolaso J Kos
Σεραφείμ,
πλέον γνωρίζεις πως ότι κάθεται καλά αισθητικά το αφήνουμε ακόμα και αν

.


Re: Η αρμονία της Fibonacci
Δημοσιεύτηκε: Πέμ Σεπ 21, 2017 9:47 am
από Σεραφείμ
 τον
τον  - οστό όρο Fibonacci και με
- οστό όρο Fibonacci και με 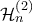 το γενικευμένο αρμονικό όρο τάξης
το γενικευμένο αρμονικό όρο τάξης  . Υπολογισθήτω:
. Υπολογισθήτω:
 τον
τον  - οστό όρο Fibonacci και με
- οστό όρο Fibonacci και με 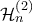 το γενικευμένο αρμονικό όρο τάξης
το γενικευμένο αρμονικό όρο τάξης  . Υπολογισθήτω:
. Υπολογισθήτω:

 , για
, για  βρέθηκαν απ’ τον Ramanujan στις αρχές του 20ου αιώνα
βρέθηκαν απ’ τον Ramanujan στις αρχές του 20ου αιώνα 
 έχουμε
έχουμε 
 (στοιχειώδες) προκύπτει
(στοιχειώδες) προκύπτει

 , θα πρέπει να γραφεί (στα πλαίσια της Πραγματικής Ανάλυσης), ως
, θα πρέπει να γραφεί (στα πλαίσια της Πραγματικής Ανάλυσης), ως  ,
,  .
.