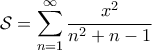 Μιας και η απάντηση αποσύρθηκε , αφού δεν απαντούσε στο αρχικό ερώτημα , θέτω ως ανεξάρτητο ερώτημα τον υπολογισμό της σειράς η οποία είναι ενδιαφέρουσα.
Μιας και η απάντηση αποσύρθηκε , αφού δεν απαντούσε στο αρχικό ερώτημα , θέτω ως ανεξάρτητο ερώτημα τον υπολογισμό της σειράς η οποία είναι ενδιαφέρουσα.Σειρούλα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Σειρούλα
Στο θέμα εδώ είχε δοθεί ο υπολογισμός της σειράς
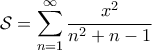 Μιας και η απάντηση αποσύρθηκε , αφού δεν απαντούσε στο αρχικό ερώτημα , θέτω ως ανεξάρτητο ερώτημα τον υπολογισμό της σειράς η οποία είναι ενδιαφέρουσα.
Μιας και η απάντηση αποσύρθηκε , αφού δεν απαντούσε στο αρχικό ερώτημα , θέτω ως ανεξάρτητο ερώτημα τον υπολογισμό της σειράς η οποία είναι ενδιαφέρουσα.
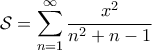 Μιας και η απάντηση αποσύρθηκε , αφού δεν απαντούσε στο αρχικό ερώτημα , θέτω ως ανεξάρτητο ερώτημα τον υπολογισμό της σειράς η οποία είναι ενδιαφέρουσα.
Μιας και η απάντηση αποσύρθηκε , αφού δεν απαντούσε στο αρχικό ερώτημα , θέτω ως ανεξάρτητο ερώτημα τον υπολογισμό της σειράς η οποία είναι ενδιαφέρουσα.Η φαντασία είναι σημαντικότερη από τη γνώση !


Λέξεις Κλειδιά:
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3055
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Σειρούλα
Θα υπολογισθεί η σειρά 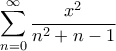 :
:
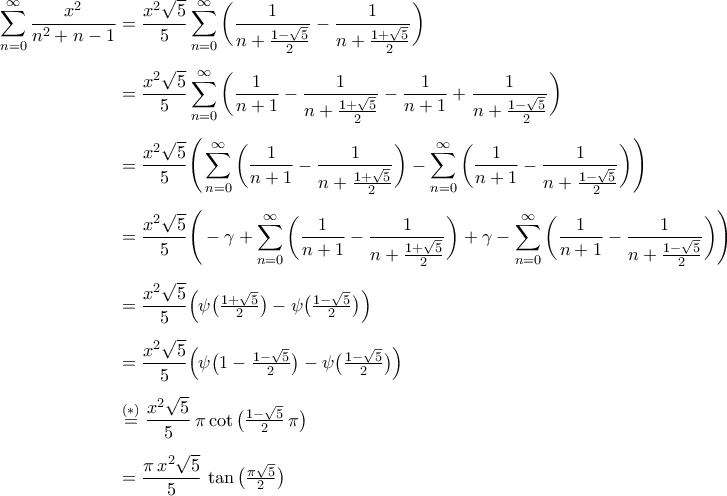
Άρα
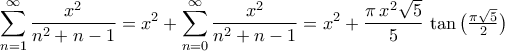
 ανακλαστικός τύπος για την
ανακλαστικός τύπος για την  .
.
Υ.Γ. Επειδή η σειρά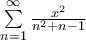 συγκλίνει, έπεται ότι και το γινόμενο
συγκλίνει, έπεται ότι και το γινόμενο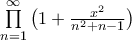 συγκλίνει.
συγκλίνει.
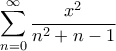 :
: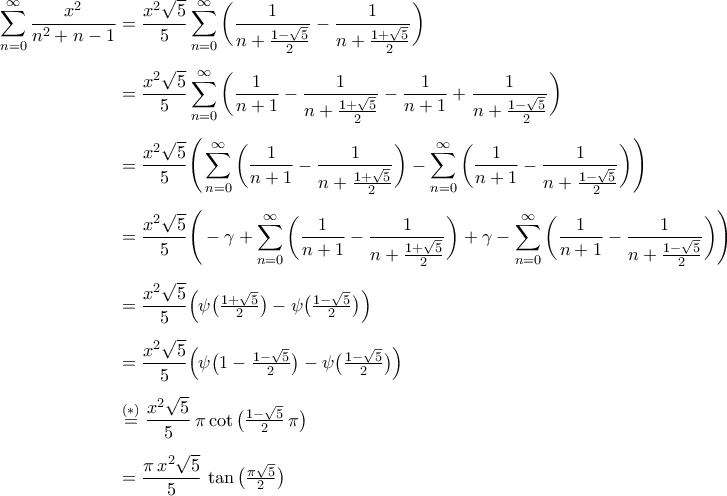
Άρα
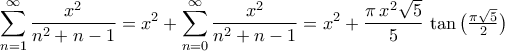
 ανακλαστικός τύπος για την
ανακλαστικός τύπος για την  .
.Υ.Γ. Επειδή η σειρά
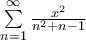 συγκλίνει, έπεται ότι και το γινόμενο
συγκλίνει, έπεται ότι και το γινόμενο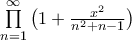 συγκλίνει.
συγκλίνει.
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρούλα
Γενικότερα για 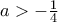 ισχύει:
ισχύει:
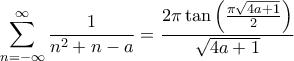 η οποία είναι μία απλή εφαρμογή του contour integration.
η οποία είναι μία απλή εφαρμογή του contour integration.
Επίσης, σε πλήρη αντιστοιχία για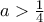 ισχύει
ισχύει
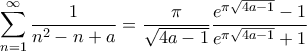 το οποίο το έχουμε δει παλιά.
το οποίο το έχουμε δει παλιά.
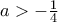 ισχύει:
ισχύει: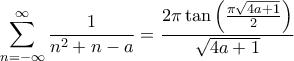 η οποία είναι μία απλή εφαρμογή του contour integration.
η οποία είναι μία απλή εφαρμογή του contour integration. Επίσης, σε πλήρη αντιστοιχία για
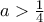 ισχύει
ισχύει 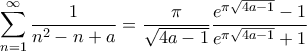 το οποίο το έχουμε δει παλιά.
το οποίο το έχουμε δει παλιά.Η φαντασία είναι σημαντικότερη από τη γνώση !


Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 23 επισκέπτες
