 με
με  .
. Να δείξετε ότι
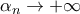 .
.Φιλικά,
Μάριος
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Το γινόμενο είναιM.S.Vovos έγραψε:Δίνεται η ακολουθίαμε
.
Να δείξετε ότι.
 και το άθροισμα
και το άθροισμα  . Όλο μαζί
. Όλο μαζί 
![\displaystyle{{\alpha _n} = \sqrt[n]{{\prod\limits_{i = 1}^n i }} - \sqrt{{\sum\limits_{i = 1}^n i }}} \displaystyle{{\alpha _n} = \sqrt[n]{{\prod\limits_{i = 1}^n i }} - \sqrt{{\sum\limits_{i = 1}^n i }}}](/forum/ext/geomar/texintegr/latexrender/pictures/a1469461a23af0f192374bc60569543f.png) .
.M.S.Vovos έγραψε: Υπολογίσατε το όριο της.
 για
για  . Πράγματι, το επαγωικό βήμα απαιτεί
. Πράγματι, το επαγωικό βήμα απαιτεί 
 που είναι το ζητούμενο.
που είναι το ζητούμενο.
![\displaystyle{ \le \sqrt [n] { \left (\frac {n}{2} \right ) ^n} - \frac {n}{\sqrt 2} = \frac {n}{2} -\frac {n}{\sqrt 2} \to - \infty \displaystyle{ \le \sqrt [n] { \left (\frac {n}{2} \right ) ^n} - \frac {n}{\sqrt 2} = \frac {n}{2} -\frac {n}{\sqrt 2} \to - \infty](/forum/ext/geomar/texintegr/latexrender/pictures/4c7686e39d11daa8c7a1390b4193237a.png)
Στην παραπάνω λύση, στο βήμαMihalis_Lambrou έγραψε:

 χρησιμοποίησα την
χρησιμοποίησα την  για
για  με
με  . Η απόδειξη αυτής είναι απλή επαγωγικά (πρόκειται για την ανισότητα Bernoulli).
. Η απόδειξη αυτής είναι απλή επαγωγικά (πρόκειται για την ανισότητα Bernoulli). ![\sqrt[n]{{\prod\limits_{i = 1}^n i }} \le \frac {1}{n} \sum\limits_{i = 1}^n i }} = \frac {n+1}{2} } \sqrt[n]{{\prod\limits_{i = 1}^n i }} \le \frac {1}{n} \sum\limits_{i = 1}^n i }} = \frac {n+1}{2} }](/forum/ext/geomar/texintegr/latexrender/pictures/ce09e91798ecb9722547a2bc173c4eac.png)
 , και λοιπά, όπως πριν.
, και λοιπά, όπως πριν. (ορισμός παραγοντικού) και
(ορισμός παραγοντικού) και  (απόδειξη με τη μέθοδο της επαγωγής ) και
(απόδειξη με τη μέθοδο της επαγωγής ) και ![\displaystyle{\frac{{\sqrt[n]{{n!}}}}{n} \to \frac{1}{e}} \displaystyle{\frac{{\sqrt[n]{{n!}}}}{n} \to \frac{1}{e}}](/forum/ext/geomar/texintegr/latexrender/pictures/51367f05a8d57bb501710883d77f9374.png) (αφήνεται ως άσκηση, έχει ενδιαφέρον).
(αφήνεται ως άσκηση, έχει ενδιαφέρον).![\displaystyle{{\alpha _n} = \sqrt[n]{{n!}} - \sqrt {\frac{{{n^2} + n}}{2}} = n\left( {\frac{{\sqrt[n]{{n!}}}}{n} - \sqrt {\frac{1}{2} + \frac{1}{{2n}}} } \right) \to + \infty \underbrace {\left( {\frac{1}{e} - \frac{1}{{\sqrt 2 }}} \right)}_{ < 0} = - \infty } \displaystyle{{\alpha _n} = \sqrt[n]{{n!}} - \sqrt {\frac{{{n^2} + n}}{2}} = n\left( {\frac{{\sqrt[n]{{n!}}}}{n} - \sqrt {\frac{1}{2} + \frac{1}{{2n}}} } \right) \to + \infty \underbrace {\left( {\frac{1}{e} - \frac{1}{{\sqrt 2 }}} \right)}_{ < 0} = - \infty }](/forum/ext/geomar/texintegr/latexrender/pictures/620373fe1650cabd69797147a3741bdc.png)
Πρόκειται για τον τύπο του Stirling, που συνήθως διατυπώνεται (η απλή του μορφή) ωςM.S.Vovos έγραψε:(αφήνεται ως άσκηση, έχει ενδιαφέρον).
![\displaystyle{\sqrt [n] {n!} \sim \frac {n}{e}} \displaystyle{\sqrt [n] {n!} \sim \frac {n}{e}}](/forum/ext/geomar/texintegr/latexrender/pictures/746430b445e44cbc35d1174eca985d8c.png) .
.![\displaystyle{\frac {\sqrt [n] {n!}}{n} \sim \frac {1}{e}} \displaystyle{\frac {\sqrt [n] {n!}}{n} \sim \frac {1}{e}}](/forum/ext/geomar/texintegr/latexrender/pictures/7fab6e4edd4ee9d29c699521a8d595c3.png) χρησιμοποίησα το πολύ απλούστερο
χρησιμοποίησα το πολύ απλούστερο ![\displaystyle{\frac {\sqrt [n] {n!}}{n} < \frac {1}{2}} \displaystyle{\frac {\sqrt [n] {n!}}{n} < \frac {1}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/eb98a39287eead8f24dac345e9c51288.png) που μας αρκεί.
που μας αρκεί.  δεν υπάρχει κανένας λόγος να βρίσκουμε ακριβείς τιμές παραστάσεων που έτσι και αλλιώς απορροφούνται από τους άλλους όρους.
δεν υπάρχει κανένας λόγος να βρίσκουμε ακριβείς τιμές παραστάσεων που έτσι και αλλιώς απορροφούνται από τους άλλους όρους. 

Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 16 επισκέπτες