 .
.Γινόμενο ημιτόνων
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Γινόμενο ημιτόνων
Βρίσκω το αριστερό μέλοςTolaso J Kos έγραψε:Ας δειχθεί ότι:.
 . Προφανώς πρόκειται για τυπογραφικό.
. Προφανώς πρόκειται για τυπογραφικό. Τα κύρια βήματα:
Είναι γνωστό (υπάρχει σε όλες τις παλιές Τριγωνομετρίες) και αποδεικνύεται εύκολα από το Θεώρημα De Moivre ότι το
 είναι πολυώνυμο βαθμού
είναι πολυώνυμο βαθμού  του
του  με πρώτο συντελεστή
με πρώτο συντελεστή  . Τώρα, για
. Τώρα, για  , οι τιμές του
, οι τιμές του  για τις οποίες ισχύει
για τις οποίες ισχύει  είναι οι
είναι οι  . Παίρνοντάς τις ανά ζεύγη, έχουμε
. Παίρνοντάς τις ανά ζεύγη, έχουμε 
άρα από την
 έπεται
έπεται
Ο ωραίος αυτός τύπος υπάρχει σε όλες τις παλιές Τριγωνομετρίες και είναι γενικότερος του ζητούμενου: Παίρνοντας όριο
 δίνει το ζητούμενο.
δίνει το ζητούμενο. Φιλικά,
Μιχάλης
Edit: Έκανα μικροαλλαγές. Αρχικά παρασύρθηκα από την εσφαλμένη εκφώνηση.
τελευταία επεξεργασία από Mihalis_Lambrou σε Παρ Ιούλ 10, 2015 11:25 pm, έχει επεξεργασθεί 3 φορές συνολικά.
-
chris_konst
- Δημοσιεύσεις: 43
- Εγγραφή: Σάβ Ιουν 13, 2015 3:03 pm
- Τοποθεσία: Χανιά
Re: Γινόμενο ημιτόνων
Θα χρησιμοποιήσουμε τον τύποTolaso J Kos έγραψε:Ας δειχθεί ότι:.

Είναι:

Όμως,
 ,
,  ,
, κλπ αντίστοιχα
 , οπότε η
, οπότε η  γίνεται:
γίνεται: 
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Γινόμενο ημιτόνων
Νομίζω ότι να παίρνουμε έναν έτοιμο, διόλου γνωστό, τύπο στο ίδιο επίπεδο πληροφορίας με το αποδεικτέο δεν είναι σωστή αντιμετώπιση της άσκησης. Με αυτή την λογική θα λύναμε όλες τις ασκήσεις που ζητούν απόδειξη τύπου απλά με το σχόλιο "είναι σωστός γιατί κάπου τον είδα¨. 'Ετσι όμως δεν βοηθάμε τον αναγνώστη ή τα Μαθηματικά.chris_konst έγραψε: Θα χρησιμοποιήσουμε τον τύπο
Έχω το ίδιο σχόλιο για την δεύτερη λύση εδώ.
Μ.
τελευταία επεξεργασία από Mihalis_Lambrou σε Παρ Ιούλ 10, 2015 11:30 pm, έχει επεξεργασθεί 2 φορές συνολικά.
- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Γινόμενο ημιτόνων
Ναι, υπάρχει. Ζητώ συγνώμη. Το σωστό είναιMihalis_Lambrou έγραψε:Βρίσκω το αριστερό μέλοςTolaso J Kos έγραψε:Ας δειχθεί ότι:.
. Υπάρχει τυπογραφικό σφάλμα;
 όπως βρήκατε και στις δύο λύσεις. Μου φύγαν κάποια νούμερα στις πράξεις.
όπως βρήκατε και στις δύο λύσεις. Μου φύγαν κάποια νούμερα στις πράξεις.Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Γινόμενο ημιτόνων
Μετά την ωραία(και διδακτική) λύση του κ.Μιχάλη,ας δούμε και τη δική μου σκέψη.
Θέτω .
.
Παρατηρώ ότι ,για κάθε
,για κάθε  φυσικό.
φυσικό.
Πολλαπλασιάζοντας από έως
έως  λαμβάνω:
λαμβάνω:
 (1).
(1).
Τώρα,θεωρώ το πολυώνυμο .Αυτό,ως γνωστόν,έχει ρίζες τις
.Αυτό,ως γνωστόν,έχει ρίζες τις  για
για  .Επιπλέον,είναι-σχεδόν-προφανές ότι οι
.Επιπλέον,είναι-σχεδόν-προφανές ότι οι  είναι συμμετρικές ως προς τον πραγματικό άξονα(τα
είναι συμμετρικές ως προς τον πραγματικό άξονα(τα  τους έχουν άθροισμα
τους έχουν άθροισμα  και τα μέτρα τους είναι ίσα),συνεπώς οι εικόνες τους ισαπέχουν απ'το
και τα μέτρα τους είναι ίσα),συνεπώς οι εικόνες τους ισαπέχουν απ'το  (του πραγματικού άξονα).Κατά συνέπεια,προκύπτει ότι
(του πραγματικού άξονα).Κατά συνέπεια,προκύπτει ότι  .
.
Επομένως,το αριστερό μέλος της (1) ισούται με και το ζητούμενο έχει αποδειχθεί(λόγω της (1)).
και το ζητούμενο έχει αποδειχθεί(λόγω της (1)).
Θέτω
 .
.Παρατηρώ ότι
 ,για κάθε
,για κάθε  φυσικό.
φυσικό.Πολλαπλασιάζοντας από
 έως
έως  λαμβάνω:
λαμβάνω: (1).
(1).Τώρα,θεωρώ το πολυώνυμο
 .Αυτό,ως γνωστόν,έχει ρίζες τις
.Αυτό,ως γνωστόν,έχει ρίζες τις  για
για  .Επιπλέον,είναι-σχεδόν-προφανές ότι οι
.Επιπλέον,είναι-σχεδόν-προφανές ότι οι  είναι συμμετρικές ως προς τον πραγματικό άξονα(τα
είναι συμμετρικές ως προς τον πραγματικό άξονα(τα  τους έχουν άθροισμα
τους έχουν άθροισμα  και τα μέτρα τους είναι ίσα),συνεπώς οι εικόνες τους ισαπέχουν απ'το
και τα μέτρα τους είναι ίσα),συνεπώς οι εικόνες τους ισαπέχουν απ'το  (του πραγματικού άξονα).Κατά συνέπεια,προκύπτει ότι
(του πραγματικού άξονα).Κατά συνέπεια,προκύπτει ότι  .
.Επομένως,το αριστερό μέλος της (1) ισούται με
 και το ζητούμενο έχει αποδειχθεί(λόγω της (1)).
και το ζητούμενο έχει αποδειχθεί(λόγω της (1)).Αντώνης Ζητρίδης
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: Γινόμενο ημιτόνων
Η απόδειξη του Αντώνη, λίγο πιο αναλυτικά:
Θεωρούμε το πολυώνυμο
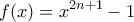
του οποίου οι ρίζες είναι οι

Μία από αυτές τις ρίζες είναι το και οι υπόλοιπες είναι ανά δύο συζυγείς.
και οι υπόλοιπες είναι ανά δύο συζυγείς.
Άρα

Επειδή
 και
και 
προκύπτει
 .
.
Διαιρώντας με προκύπτει
προκύπτει

Θέτοντας τώρα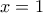 βρίσκουμε
βρίσκουμε

η οποία, με χρήση της ταυτότητας δίνει τη ζητούμενη.
δίνει τη ζητούμενη.
Θεωρούμε το πολυώνυμο
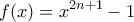
του οποίου οι ρίζες είναι οι

Μία από αυτές τις ρίζες είναι το
 και οι υπόλοιπες είναι ανά δύο συζυγείς.
και οι υπόλοιπες είναι ανά δύο συζυγείς.Άρα

Επειδή
 και
και 
προκύπτει
 .
.Διαιρώντας με
 προκύπτει
προκύπτει
Θέτοντας τώρα
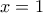 βρίσκουμε
βρίσκουμε
η οποία, με χρήση της ταυτότητας
 δίνει τη ζητούμενη.
δίνει τη ζητούμενη.Μάγκος Θάνος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 22 επισκέπτες
