Σύγκλιση ακολουθίας
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Re: Σύγκλιση ακολουθίας
...εχεις δικιο παρασυρθηκα απο σειρες (οχι εναλλασσουσες)
θελουν φρεσκαρισμα..
ενταξει με latex ευχαριστω demetres!
θελουν φρεσκαρισμα..
ενταξει με latex ευχαριστω demetres!
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Σύγκλιση ακολουθίας
Ροδόλφε,R BORIS έγραψε:Να εξεταστεί ως προς την σύγκλιση η ακολουθία
Είναι (νομίζω) μια καλή άσκηση από τα φοιτητικά μου χρόνια
μόλις τώρα βλέπω την άσκηση. Εϊναι υπέροχη ! Αμυδρά κάτι μου έρχεται στο μυαλό μου , διότι είχα και γω χρησιμοποιήσει το βιβλίο των Ηardy - Wright , αλλά δεν μπορώ να θυμηθώ τίποτα. Μου φαίνεται ότι είχα συναντήσει και στο ΑΙΘΡΑ (βιβλιοπωλείο του Ε.Σπανδάγου) έναν καθηγητή από το Μαθηματικό Αθήνας και κάτι είχαμε κουβεντιάσει .
Τέλος πάντων, μια και ασχολήστε εσείς , να μην εμπλακώ και γω. Όλη η υπόθεση είναι να βρούμε ένα αριστερό φράγμα του υπόρριζου ή κάτι τέτοιο. Θα περιμένω με αγωνία τις τελικές προτάσεις .Καλή συνέχεια.
Μπάμπης
-
ttheodoros
- Δημοσιεύσεις: 83
- Εγγραφή: Κυρ Νοέμ 21, 2010 4:28 pm
- Τοποθεσία: Λευκωσία - Κύπρος
- Γ.-Σ. Σμυρλής
- Δημοσιεύσεις: 578
- Εγγραφή: Κυρ Οκτ 14, 2012 9:47 am
- Τοποθεσία: Λευκωσία, Κύπρος
Re: Σύγκλιση ακολουθίας
Δέκα χρόνια μετὰ τὴν ὑποβολή:
Σύμφωνα μὲ τὴν εργασία:
Salikhov, V. Kh., On the Irrationality Measure of π, Usp. Mat. Nauk 63, 163-164, 2008. English transl. [Russ. Math. Surv 63, 570-572, 2008.]
Τὸ μέτρον ἀρρητότητος (measure of irrationality) τοῦ π είναι μικρότερον τοῦ 7.6063. Αὐτὸ ἔχει ὡς συνέπεια ὅτι:
Γιὰ ἐπαρκῶς μεγάλο
ἐπαρκῶς μεγάλο

διὰ κάθε καὶ ἄρα
καὶ ἄρα

διὰ κάθε .
.
Ἐπίσης, ἂν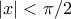 , τότε
, τότε

Ἔστω τώρα

καὶ ἔστω , ὥστε νὰ ἐλαχιστοποιεῖται ἡ τιμὴ τοῦ
, ὥστε νὰ ἐλαχιστοποιεῖται ἡ τιμὴ τοῦ 
ὁπότε εὔκολα διαπιστοῦται ὅτι

Τότε, γιὰ ἀρκετὰ μεγὰλο

γιὰ κάποιο , καὶ χάριν τῆς (2),
, καὶ χάριν τῆς (2),

γιὰ κάποιο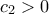 καὶ ἄρα ἐν τέλει
καὶ ἄρα ἐν τέλει
![\displaystyle{
\lim_{n\to\infty}\sqrt[n]{1+\sin n}=1.
} \displaystyle{
\lim_{n\to\infty}\sqrt[n]{1+\sin n}=1.
}](/forum/ext/geomar/texintegr/latexrender/pictures/b4585009a367a60985ddc5c3b4158fc3.png)
For more see http://mathworld.wolfram.com/IrrationalityMeasure.html
Σύμφωνα μὲ τὴν εργασία:
Salikhov, V. Kh., On the Irrationality Measure of π, Usp. Mat. Nauk 63, 163-164, 2008. English transl. [Russ. Math. Surv 63, 570-572, 2008.]
Τὸ μέτρον ἀρρητότητος (measure of irrationality) τοῦ π είναι μικρότερον τοῦ 7.6063. Αὐτὸ ἔχει ὡς συνέπεια ὅτι:
Γιὰ
 ἐπαρκῶς μεγάλο
ἐπαρκῶς μεγάλο
διὰ κάθε
 καὶ ἄρα
καὶ ἄρα
διὰ κάθε
 .
.Ἐπίσης, ἂν
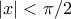 , τότε
, τότε
Ἔστω τώρα

καὶ ἔστω
 , ὥστε νὰ ἐλαχιστοποιεῖται ἡ τιμὴ τοῦ
, ὥστε νὰ ἐλαχιστοποιεῖται ἡ τιμὴ τοῦ 
ὁπότε εὔκολα διαπιστοῦται ὅτι

Τότε, γιὰ ἀρκετὰ μεγὰλο


γιὰ κάποιο
 , καὶ χάριν τῆς (2),
, καὶ χάριν τῆς (2),
γιὰ κάποιο
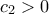 καὶ ἄρα ἐν τέλει
καὶ ἄρα ἐν τέλει![\displaystyle{
\lim_{n\to\infty}\sqrt[n]{1+\sin n}=1.
} \displaystyle{
\lim_{n\to\infty}\sqrt[n]{1+\sin n}=1.
}](/forum/ext/geomar/texintegr/latexrender/pictures/b4585009a367a60985ddc5c3b4158fc3.png)
For more see http://mathworld.wolfram.com/IrrationalityMeasure.html
Re: Σύγκλιση ακολουθίας
13 χρόνια μετά την δημοσίευση του προβλήματος... για το αρχείο...
Το πρόβλημα ειχε δημοσιευθεί στην Διάσταση (ΕΜΕ Κ. Μακεδονίας) το 92-93 (περίπου) και ρωτούσε αν έχαι λύση στοιχειώδη (π.χ. χωρίς χρήση του μέτρου αρρητότητας του π).
Μετά από αρκετές προσπάθειες μαθηματικών για στοιχειώδη αντιμετώπιση, που δεν ευδοκίμησε, ο αείμνηστος πανεπιστημιακός Ν. Δανίκας έδωσε λύση με μιγαδικούς (επίσης στην Διάσταση, πολύ παρόμοια στην ουσία με μία απο τις παραπάνω) χρησιμοποιώντας το 42 (από θεώρημα του Mahler (1953) για το μέτρο αρρητότητας του π). Αυτό έχει βελτιωθεί κατά πολύ όπως αναφέρει ο Γιώργος και είναι τώρα στο ~7.1 μετά το 2020.
Σαν σχόλιο, δεν πιστεύω προσωπικά ότι υπάρχει στοιχειώδης λύση! Τουλάχιστον όχι ευπρόσιτη. Το πρόβλημα περιλαμβάνεται στην υπέροχη συλλογή προβλημάτων "Problems in Mathematical Analysis" των Biler, Witkowski, ως πρόβλημα 2.34 με μικρή αναδιατύπωση: Βρείτε το
Κατά καιρούς το έχω ρωτήσει σε αρκετούς μαθηματικούς και οι απαντήσεις "δεν υπάρχει το όριο" ή "είναι προφανώς 1" ήταν πολύ περισσότερες...
ΥΓ: Αν και ίσως να μην μου επιτρέπεται δεοντολογικά... λόγω του ότι είμαι ακόμα "αρχάριος" μαθηματικός... είμαι έτοιμος να δώσω €100 για "στοιχειώδη" λύση του παραπάνω γρίφου, όπου π.χ. το 42 για το μέτρο του π ή ό,τι αντίστοιχο (αν χρησιμοποιείται βέβαια) αποδεικνύεται καθαρά.
Το πρόβλημα ειχε δημοσιευθεί στην Διάσταση (ΕΜΕ Κ. Μακεδονίας) το 92-93 (περίπου) και ρωτούσε αν έχαι λύση στοιχειώδη (π.χ. χωρίς χρήση του μέτρου αρρητότητας του π).
Μετά από αρκετές προσπάθειες μαθηματικών για στοιχειώδη αντιμετώπιση, που δεν ευδοκίμησε, ο αείμνηστος πανεπιστημιακός Ν. Δανίκας έδωσε λύση με μιγαδικούς (επίσης στην Διάσταση, πολύ παρόμοια στην ουσία με μία απο τις παραπάνω) χρησιμοποιώντας το 42 (από θεώρημα του Mahler (1953) για το μέτρο αρρητότητας του π). Αυτό έχει βελτιωθεί κατά πολύ όπως αναφέρει ο Γιώργος και είναι τώρα στο ~7.1 μετά το 2020.
Σαν σχόλιο, δεν πιστεύω προσωπικά ότι υπάρχει στοιχειώδης λύση! Τουλάχιστον όχι ευπρόσιτη. Το πρόβλημα περιλαμβάνεται στην υπέροχη συλλογή προβλημάτων "Problems in Mathematical Analysis" των Biler, Witkowski, ως πρόβλημα 2.34 με μικρή αναδιατύπωση: Βρείτε το

Κατά καιρούς το έχω ρωτήσει σε αρκετούς μαθηματικούς και οι απαντήσεις "δεν υπάρχει το όριο" ή "είναι προφανώς 1" ήταν πολύ περισσότερες...
ΥΓ: Αν και ίσως να μην μου επιτρέπεται δεοντολογικά... λόγω του ότι είμαι ακόμα "αρχάριος" μαθηματικός... είμαι έτοιμος να δώσω €100 για "στοιχειώδη" λύση του παραπάνω γρίφου, όπου π.χ. το 42 για το μέτρο του π ή ό,τι αντίστοιχο (αν χρησιμοποιείται βέβαια) αποδεικνύεται καθαρά.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες

![a_n=\sqrt[n]{1+sin(n)} a_n=\sqrt[n]{1+sin(n)}](/forum/ext/geomar/texintegr/latexrender/pictures/67c900f4347a2ff6990b860f14e43034.png)