Σημεία ασυνέχειας
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Σημεία ασυνέχειας
Αν η συνάρτηση f ορίζεται στο διάστημα [0,1] και παίρνει κάθε τιμή της ακριβώς δύο φορές, να δειχθεί ότι έχει άπειρα σημεία ασυνέχειας
Σημείωση: Δεν έχω λύση
Σημείωση: Δεν έχω λύση
Σπύρος Καπελλίδης
Λέξεις Κλειδιά:
Re: Σημεία ασυνέχειας
Πολύ όμορφη άσκηση. Θα δώσω μία 'σκιαγράφηση' της λύσης διότι το
τεχνικό κομμάτι είναι μεγάλο. Αρχικά ορίζουμε τη συνάρτηση
![g:[0,1]\to [0,1] g:[0,1]\to [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/97fd26d67e9595db275d4a69efc1fd5b.png) με
με  , όπου
, όπου  με
με  .
.
Προφανώς η συνάρτηση αυτή είναι καλά ορισμένη με![Dom(g)=[0,1] Dom(g)=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/bddbd245fe97c9db0e9e0b713e4ded99.png) και
και ![Range(g)=[0,1] Range(g)=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/a25d0b490cdefc79109790d1ce1aa7ef.png) .
.
Επίσης πρέπει για κάθε
για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) και φυσικά
και φυσικά  για κάθε
για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) .
.
Εύκολα μπορούμε να δείξουμε ότι αν η είναι συνεχής στα
είναι συνεχής στα  με
με  ,
,
τότε η είναι συνεχής στο
είναι συνεχής στο 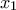 . Άρα αν η
. Άρα αν η  είναι ασυνεχής στο
είναι ασυνεχής στο 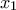 , τότε η
, τότε η  είναι ασυνεχής
είναι ασυνεχής
είτε στο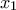 είτε στο
είτε στο  . Θα δείξουμε ότι η
. Θα δείξουμε ότι η  είναι ασυνεχής σε άπειρα σημεία. Καταρχήν είναι προφανές
είναι ασυνεχής σε άπειρα σημεία. Καταρχήν είναι προφανές
ότι η είναι ασυνεχής σε τουλάχιστον ένα σημείο. Παρατηρούμε ότι
είναι ασυνεχής σε τουλάχιστον ένα σημείο. Παρατηρούμε ότι  αν και μόνο αν
αν και μόνο αν  ,
,
άρα αν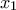 σημείο ασυνέχειας της
σημείο ασυνέχειας της  , τότε το
, τότε το  θα είναι επίσης σημείο ασυνέχειας της
θα είναι επίσης σημείο ασυνέχειας της  .
.
Έστω , τότε η
, τότε η  δεν μπορεί να είναι συνεχής στο διάστημα
δεν μπορεί να είναι συνεχής στο διάστημα 
διότι τα σημεία και
και  βρίσκονται εκατέρωθεν της ευθείας
βρίσκονται εκατέρωθεν της ευθείας 
που δεν μπορεί να τέμνεται από την . Επομένως η
. Επομένως η  είναι ασυνεχής σε άπειρα σημεία.
είναι ασυνεχής σε άπειρα σημεία.
τεχνικό κομμάτι είναι μεγάλο. Αρχικά ορίζουμε τη συνάρτηση
![g:[0,1]\to [0,1] g:[0,1]\to [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/97fd26d67e9595db275d4a69efc1fd5b.png) με
με  , όπου
, όπου  με
με  .
. Προφανώς η συνάρτηση αυτή είναι καλά ορισμένη με
![Dom(g)=[0,1] Dom(g)=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/bddbd245fe97c9db0e9e0b713e4ded99.png) και
και ![Range(g)=[0,1] Range(g)=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/a25d0b490cdefc79109790d1ce1aa7ef.png) .
. Επίσης πρέπει
 για κάθε
για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) και φυσικά
και φυσικά  για κάθε
για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) .
. Εύκολα μπορούμε να δείξουμε ότι αν η
 είναι συνεχής στα
είναι συνεχής στα  με
με  ,
,τότε η
 είναι συνεχής στο
είναι συνεχής στο 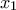 . Άρα αν η
. Άρα αν η  είναι ασυνεχής στο
είναι ασυνεχής στο 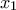 , τότε η
, τότε η  είναι ασυνεχής
είναι ασυνεχής είτε στο
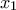 είτε στο
είτε στο  . Θα δείξουμε ότι η
. Θα δείξουμε ότι η  είναι ασυνεχής σε άπειρα σημεία. Καταρχήν είναι προφανές
είναι ασυνεχής σε άπειρα σημεία. Καταρχήν είναι προφανές ότι η
 είναι ασυνεχής σε τουλάχιστον ένα σημείο. Παρατηρούμε ότι
είναι ασυνεχής σε τουλάχιστον ένα σημείο. Παρατηρούμε ότι  αν και μόνο αν
αν και μόνο αν  ,
, άρα αν
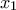 σημείο ασυνέχειας της
σημείο ασυνέχειας της  , τότε το
, τότε το  θα είναι επίσης σημείο ασυνέχειας της
θα είναι επίσης σημείο ασυνέχειας της  .
.Έστω
 , τότε η
, τότε η  δεν μπορεί να είναι συνεχής στο διάστημα
δεν μπορεί να είναι συνεχής στο διάστημα 
διότι τα σημεία
 και
και  βρίσκονται εκατέρωθεν της ευθείας
βρίσκονται εκατέρωθεν της ευθείας 
που δεν μπορεί να τέμνεται από την
 . Επομένως η
. Επομένως η  είναι ασυνεχής σε άπειρα σημεία.
είναι ασυνεχής σε άπειρα σημεία.1. Mathematics is the language of nature.
2. Everything around us can be represented and understood through numbers.
3. If you graph these numbers of any system patterns emerge.
Therefore: There are patterns everywhere in nature.
2. Everything around us can be represented and understood through numbers.
3. If you graph these numbers of any system patterns emerge.
Therefore: There are patterns everywhere in nature.
-
mtsarduckas
- Δημοσιεύσεις: 106
- Εγγραφή: Πέμ Απρ 09, 2009 9:44 am
- Τοποθεσία: Αθήνα
Re: Σημεία ασυνέχειας
Πανέμορφη άσκηση και ακόμα πιο όμορφη λύση  . Προσωπικά πάλεψα για ένα δίωρο να δείξω ότι το σύνολο των σημείων ασυνέχειας της f είναι πεπερασμένο αλλά χωρίς επιτυχία...
. Προσωπικά πάλεψα για ένα δίωρο να δείξω ότι το σύνολο των σημείων ασυνέχειας της f είναι πεπερασμένο αλλά χωρίς επιτυχία... 
Re: Σημεία ασυνέχειας
Σε ευχαριστώ Paulgal μου έλυσες ένα πρόβλημα που με απασχολούσε καιρό.
Σπύρος Καπελλίδης
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Σημεία ασυνέχειας
paulgai, έχω τις επιφυλάξεις μου για τον τελευταίο συλλογισμό. Μπορεί να μη βλέπω κάτι απλό, πάντως δεν το βλέπω.paulgai έγραψε: Έστω, τότε η
δεν μπορεί να είναι συνεχής στο διάστημα
διότι τα σημείακαι
βρίσκονται εκατέρωθεν της ευθείας

που δεν μπορεί να τέμνεται από την. Επομένως η
είναι ασυνεχής σε άπειρα σημεία.
Λέμε: αρχίζουμε με x1< x2 τετοια ώστε f(x1) = f(x2) και εξετάζουμε το διάστημα (x1, x2). Eκεί έχουμε ασυνέχεια, οπότε βρίσκουμε σημείο ασυνέχειας x3 στο εσωτερικό του. Μεταξύ του x3 και του αντίστοιχου x4 με f(x3)=f(x4) βρίσκουμε νέο σημείο ασυνέχειας και ούτω καθ' εξής. Πες όμως ότι είχαμε x1 < x3 < x2 < x4. Ποιός μου εξασφαλίζει ότι το σημείο ασυνέχειας που θα βρούμε στο (x3, x4) δεν είναι πάλι το x2 ; Γιατί πρέπει να είναι νέο σημείο;
Υποθέτω ότι διορθώνεται αυτό, αλλά κάτι λείπει.
Φιλικά,
Μιχάλης Λάμπρου
Re: Σημεία ασυνέχειας
Σωστότατη η παρατήρησή σας κύριε Λάμπρου. Θα προσπαθήσω ναMihalis_Lambrou έγραψε:paulgai, έχω τις επιφυλάξεις μου για τον τελευταίο συλλογισμό. Μπορεί να μη βλέπω κάτι απλό, πάντως δεν το βλέπω.paulgai έγραψε: Έστω, τότε η
δεν μπορεί να είναι συνεχής στο διάστημα
διότι τα σημείακαι
βρίσκονται εκατέρωθεν της ευθείας

που δεν μπορεί να τέμνεται από την. Επομένως η
είναι ασυνεχής σε άπειρα σημεία.
Λέμε: αρχίζουμε με x1< x2 τετοια ώστε f(x1) = f(x2) και εξετάζουμε το διάστημα (x1, x2). Eκεί έχουμε ασυνέχεια, οπότε βρίσκουμε σημείο ασυνέχειας x3 στο εσωτερικό του. Μεταξύ του x3 και του αντίστοιχου x4 με f(x3)=f(x4) βρίσκουμε νέο σημείο ασυνέχειας και ούτω καθ' εξής. Πες όμως ότι είχαμε x1 < x3 < x2 < x4. Ποιός μου εξασφαλίζει ότι το σημείο ασυνέχειας που θα βρούμε στο (x3, x4) δεν είναι πάλι το x2 ; Γιατί πρέπει να είναι νέο σημείο;
Υποθέτω ότι διορθώνεται αυτό, αλλά κάτι λείπει.
Φιλικά,
Μιχάλης Λάμπρου
συμπληρώσω το λογικό κενό. Αν
 ονομάσω την περιοχή των
ονομάσω την περιοχή των σημείων του
![[0,1]^{2} [0,1]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/514392e7ca5fed0c25ab1ea0b6b6b045.png) με
με  και
και  την περιοχή των σημείων του
την περιοχή των σημείων του ![[0,1]^{2} [0,1]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/514392e7ca5fed0c25ab1ea0b6b6b045.png) με
με  , τότε αν
, τότε αν  θα ισχύει
θα ισχύει  και
και  . Έστω, όπως είπατε,
. Έστω, όπως είπατε,  σημείο ασυνέχειας με
σημείο ασυνέχειας με  με
με 
και
 . Αν το
. Αν το  , τότε αφού
, τότε αφού το
 θα έχουμε νέο σημείο ασυνέχειας στο διάστημα
θα έχουμε νέο σημείο ασυνέχειας στο διάστημα  , αν πάλι το
, αν πάλι το  τότε αφού το
τότε αφού το 
θα έχουμε νέο σημείο ασυνέχειας στο διάστημα
 .
.Edit: Έγινε διόρθωση σε ένα λάθος που είχα κάνει.
Υ.Γ. Nομίζω ότι αναγκαστικά θα ισχύει
 , αν και αυτό δεν έχει πολύ σημασία.
, αν και αυτό δεν έχει πολύ σημασία.1. Mathematics is the language of nature.
2. Everything around us can be represented and understood through numbers.
3. If you graph these numbers of any system patterns emerge.
Therefore: There are patterns everywhere in nature.
2. Everything around us can be represented and understood through numbers.
3. If you graph these numbers of any system patterns emerge.
Therefore: There are patterns everywhere in nature.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Σημεία ασυνέχειας
Νομίζω με αυτήν την διόρθωση η απόδειξη είναι πλέον σωστή.paulgai έγραψε:Σωστότατη η παρατήρησή σας κύριε Λάμπρου. Θα προσπαθήσω ναMihalis_Lambrou έγραψε:paulgai, έχω τις επιφυλάξεις μου για τον τελευταίο συλλογισμό. Μπορεί να μη βλέπω κάτι απλό, πάντως δεν το βλέπω.paulgai έγραψε: Έστω, τότε η
δεν μπορεί να είναι συνεχής στο διάστημα
διότι τα σημείακαι
βρίσκονται εκατέρωθεν της ευθείας

που δεν μπορεί να τέμνεται από την. Επομένως η
είναι ασυνεχής σε άπειρα σημεία.
Λέμε: αρχίζουμε με x1< x2 τετοια ώστε f(x1) = f(x2) και εξετάζουμε το διάστημα (x1, x2). Eκεί έχουμε ασυνέχεια, οπότε βρίσκουμε σημείο ασυνέχειας x3 στο εσωτερικό του. Μεταξύ του x3 και του αντίστοιχου x4 με f(x3)=f(x4) βρίσκουμε νέο σημείο ασυνέχειας και ούτω καθ' εξής. Πες όμως ότι είχαμε x1 < x3 < x2 < x4. Ποιός μου εξασφαλίζει ότι το σημείο ασυνέχειας που θα βρούμε στο (x3, x4) δεν είναι πάλι το x2 ; Γιατί πρέπει να είναι νέο σημείο;
Υποθέτω ότι διορθώνεται αυτό, αλλά κάτι λείπει.
Φιλικά,
Μιχάλης Λάμπρου
συμπληρώσω το λογικό κενό. Ανονομάσω την περιοχή των
σημείων τουμε
και
την περιοχή των σημείων του
με
, τότε αν
θα ισχύει
και
. Έστω, όπως είπατε,
σημείο ασυνέχειας με
με

και. Αν το
, τότε αφού
τοθα έχουμε νέο σημείο ασυνέχειας στο διάστημα
, αν πάλι το
τότε αφού το
θα έχουμε νέο σημείο ασυνέχειας στο διάστημα.
Edit: Έγινε διόρθωση σε ένα λάθος που είχα κάνει.
Υ.Γ. Nομίζω ότι αναγκαστικά θα ισχύει, αν και αυτό δεν έχει πολύ σημασία.
Ας την γράψω λίγο διαφορετικά. Αρκεί να δείξουμε ότι η
 είναι ασυνεχής σε άπειρα σημεία. Ας υποθέσουμε πως αυτό δεν αληθεύει και τα
είναι ασυνεχής σε άπειρα σημεία. Ας υποθέσουμε πως αυτό δεν αληθεύει και τα  είναι τα μόνα σημεία ασυνέχειας της
είναι τα μόνα σημεία ασυνέχειας της  .
. Αν
 τότε, επειδή
τότε, επειδή  και
και  θα υπάρχει σημείο ασυνέχειας στο διάστημα
θα υπάρχει σημείο ασυνέχειας στο διάστημα  , άτοπο.
, άτοπο.Άρα
 . (1)
. (1)Αν
 τότε, επειδή
τότε, επειδή  και
και  θα υπάρχει σημείο ασυνέχειας στο διάστημα
θα υπάρχει σημείο ασυνέχειας στο διάστημα  , άτοπο.
, άτοπο.Άρα
 (2)
(2)Από τα (1) και (2) συμπεραίνουμε ότι θα υπάρχει
 ώστε
ώστε  και
και  . Αλλά τότε, επειδή
. Αλλά τότε, επειδή  και
και  θα υπάρχει σημείο ασυνέχειας στο διάστημα
θα υπάρχει σημείο ασυνέχειας στο διάστημα  , άτοπο.
, άτοπο.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες
