
Σειρά 2.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Re: Σειρά 2.
Μαγικό ........
![\displaystyle{\displaystyle4\sum_{n=1}^{\infty}\frac{(-1)^{n-1}(2n-1)}{(2n-1)^2-4a^2}=4\frac{1}{2}\left[\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};-a+\frac{1}{2}\right)+\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};a+\frac{1}{2}\right)\right]=} \displaystyle{\displaystyle4\sum_{n=1}^{\infty}\frac{(-1)^{n-1}(2n-1)}{(2n-1)^2-4a^2}=4\frac{1}{2}\left[\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};-a+\frac{1}{2}\right)+\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};a+\frac{1}{2}\right)\right]=}](/forum/ext/geomar/texintegr/latexrender/pictures/6fc5925122336f485643fb3377e806a7.png)
![\displaystyle{2\left[\frac{1}{4} \pi \sec (\pi a)+\frac{1}{4} \pi \sec (\pi a)\right]=\pi\sec(\pi a )=\frac{\pi}{\cos(\pi a )}} \displaystyle{2\left[\frac{1}{4} \pi \sec (\pi a)+\frac{1}{4} \pi \sec (\pi a)\right]=\pi\sec(\pi a )=\frac{\pi}{\cos(\pi a )}}](/forum/ext/geomar/texintegr/latexrender/pictures/5599fb7b23604d981555823bea7cf829.png)
Το παραπάνω προκύπτει με ολοκλήρωση επί του τετραγώνου με κέντρο την αρχή των αξόνων του μιγαδικού επιπέδου, είναι λίγο αργά και θα μπω σε λεπτομέρειες αύριο (θέλει και σχήμα)..... παρ´όλα αυτά alea iacta est.
.
![\displaystyle{\displaystyle4\sum_{n=1}^{\infty}\frac{(-1)^{n-1}(2n-1)}{(2n-1)^2-4a^2}=4\frac{1}{2}\left[\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};-a+\frac{1}{2}\right)+\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};a+\frac{1}{2}\right)\right]=} \displaystyle{\displaystyle4\sum_{n=1}^{\infty}\frac{(-1)^{n-1}(2n-1)}{(2n-1)^2-4a^2}=4\frac{1}{2}\left[\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};-a+\frac{1}{2}\right)+\textrm{Residue}\left(\frac{\pi\csc(\pi z )(2z-1)}{(2z-1)^2-4a^2};a+\frac{1}{2}\right)\right]=}](/forum/ext/geomar/texintegr/latexrender/pictures/6fc5925122336f485643fb3377e806a7.png)
![\displaystyle{2\left[\frac{1}{4} \pi \sec (\pi a)+\frac{1}{4} \pi \sec (\pi a)\right]=\pi\sec(\pi a )=\frac{\pi}{\cos(\pi a )}} \displaystyle{2\left[\frac{1}{4} \pi \sec (\pi a)+\frac{1}{4} \pi \sec (\pi a)\right]=\pi\sec(\pi a )=\frac{\pi}{\cos(\pi a )}}](/forum/ext/geomar/texintegr/latexrender/pictures/5599fb7b23604d981555823bea7cf829.png)
Το παραπάνω προκύπτει με ολοκλήρωση επί του τετραγώνου με κέντρο την αρχή των αξόνων του μιγαδικού επιπέδου, είναι λίγο αργά και θα μπω σε λεπτομέρειες αύριο (θέλει και σχήμα)..... παρ´όλα αυτά alea iacta est.
.
What's wrong with a Greek in Hamburg?
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Σειρά 2.
Μετά την τηλεγραφική λύση του Γιώργου, για την οποία περιμένουμε επεξηγήσεις, ακόμα μια λύση με Αναλυτική Θεωρία Αριθμών.





-----------------------------------------------------------------------------------------------------------------------------------------------
Χρησιμοποιήθηκε η σχέση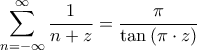 που αποδείχθηκε εδώ viewtopic.php?f=9&t=24766
που αποδείχθηκε εδώ viewtopic.php?f=9&t=24766
Άκουσα πως υπάρχει και μια λύση με σειρές Fourier .. αναμένουμε ..





-----------------------------------------------------------------------------------------------------------------------------------------------
Χρησιμοποιήθηκε η σχέση
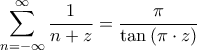 που αποδείχθηκε εδώ viewtopic.php?f=9&t=24766
που αποδείχθηκε εδώ viewtopic.php?f=9&t=24766Άκουσα πως υπάρχει και μια λύση με σειρές Fourier .. αναμένουμε ..
Σεραφείμ Τσιπέλης
- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σειρά 2.
Γεια σου Σεραφείμ. Μετά από
 χρόνια βέβαια η απάντηση αλλά νομίζω ότι το ακόλουθο απαντάει στο ερώτημά σου.
χρόνια βέβαια η απάντηση αλλά νομίζω ότι το ακόλουθο απαντάει στο ερώτημά σου.![\displaystyle{\sin ax = \left\{\begin{matrix}
\displaystyle \frac{4a}{\pi} \sum_{n=0}^{\infty} \frac{\cos (2n+1)x}{a^2-\left ( 2n+1 \right )^2} & , & a \quad \text{\gr άρτιος} \\\\
\displaystyle \frac{4a}{\pi} \left [ \frac{1}{2a^2} + \sum_{n=1}^{\infty} \frac{\cos 2nx}{a^2-4n^2} \right ]& , & a \quad \text{\gr περιττός}
\end{matrix}\right.} \displaystyle{\sin ax = \left\{\begin{matrix}
\displaystyle \frac{4a}{\pi} \sum_{n=0}^{\infty} \frac{\cos (2n+1)x}{a^2-\left ( 2n+1 \right )^2} & , & a \quad \text{\gr άρτιος} \\\\
\displaystyle \frac{4a}{\pi} \left [ \frac{1}{2a^2} + \sum_{n=1}^{\infty} \frac{\cos 2nx}{a^2-4n^2} \right ]& , & a \quad \text{\gr περιττός}
\end{matrix}\right.}](/forum/ext/geomar/texintegr/latexrender/pictures/3beae84b062e80b80c8f7c7a2a8d8801.png) όπου φυσικά
όπου φυσικά  και
και  .
.Η φαντασία είναι σημαντικότερη από τη γνώση !


-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Σειρά 2.
Είναι

για

Βάζοντας όπου
 το
το  και για
και για 
παίρνουμε το άθροισμα.
Συμπλήρωμα.Ελπίζω να μην πιστεύει κανείς ότι θυμόμουν τον τύπο.Απλά ήξερα ότι κάτι παρόμοιο υπάρχει και έψαξα και τον
βρήκα.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες
