Δίνεται η συνάρτηση
 με m ακέραιο. Να αποδειχθεί ότι τα σημεία τοπικών ακροτάτων της f δινονται από την εξίσωση mσυν(mx)ημx=ημ(mx)συνx και να συμπεράνετε ότι
με m ακέραιο. Να αποδειχθεί ότι τα σημεία τοπικών ακροτάτων της f δινονται από την εξίσωση mσυν(mx)ημx=ημ(mx)συνx και να συμπεράνετε ότι  .
.Υ.Γ.Μπορει να μην στεκεται στο ύψος μιας Ολυμπιάδας αλλά ενδεχομένως για ενα μαθηματικό διαγωνισμό..
Μετά από την εύστοχη παρατηρηση του Δημητρη Σκουτερη ότι για περιττες τιμες του m δεν οριζεται η εφαπτομένη διορθωσα το επίμαχο σημειο.Ευχαριστώ Δημήτρη.

 ή
ή  , η άσκηση προκύπτει εύκολα. Έστω, λοιπόν,
, η άσκηση προκύπτει εύκολα. Έστω, λοιπόν,  .
. είναι το
είναι το  .
. με
με
 .
. στο
στο 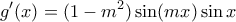
 είναι στο
είναι στο  , τότε
, τότε 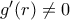 .
. , οπότε αν
, οπότε αν  , τότε θα πρέπει
, τότε θα πρέπει  . Αλλά τότε
. Αλλά τότε  , άτοπο).
, άτοπο). τέτοιο ώστε η
τέτοιο ώστε η  έχει σταθερό πρόσημο στο
έχει σταθερό πρόσημο στο  . Δηλαδή, ή
. Δηλαδή, ή  για κάθε
για κάθε  ή
ή  για κάθε
για κάθε  , παίρνουμε
, παίρνουμε  για κάθε
για κάθε 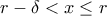 , και
, και  για κάθε
για κάθε  .
. .
.  .
. αποδεικνύεται πολύ εύκολα με επαγωγή στο
αποδεικνύεται πολύ εύκολα με επαγωγή στο  .
.