Αφού το σημείο είναι κανονικό ανώμαλο, αναζητούμε τη λύση (στην περιοχή του

) στη μορφή
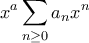
με

.
Αντικαθιστώντας στη διαφορική θα πάρουμε
![\displaystyle{(a^2-2a)a_{0}x^{a-2}+(a^2-1)a_{1}x^{a-1}+(\color{red}a^2+2a\color{black})a_{2}x^a+\sum_{n\geq0}\left[\left(n^2+(4+2a)n+a^2+4a+3\right)a_{n+3}+4a_{n}\right]x^{n+a+1}=0} \displaystyle{(a^2-2a)a_{0}x^{a-2}+(a^2-1)a_{1}x^{a-1}+(\color{red}a^2+2a\color{black})a_{2}x^a+\sum_{n\geq0}\left[\left(n^2+(4+2a)n+a^2+4a+3\right)a_{n+3}+4a_{n}\right]x^{n+a+1}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/7ee82ab7fcf50802a1692ec25394af66.png)
Εξισώνοντας τον πρώτο συντελεστή με το

και αφού

, παίρνουμε

ή
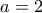
.
Η πρώτη περίπτωση θα δώσει
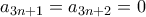
για

και

για

.
Άρα η μια λύση θα είναι η 
Για
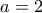
θα κάνεις τα αντίστοιχα για να πάρεις τη δεύτερη λύση.
Ένα ωραίο βιβλίο με κάμποσα παραδείγματα για αυτά είναι το Advanced Mathematical Methods for Scientists and Engineers (Asymptotic Methods and Perturbation Theory) των C.M.Bender και S.A.Orszag. Υπάρχει στο δίκτυο.
Διόρθωσα τυπογραφικό. Το αποτέλεσμα όμως παραμένει το ίδιο.


 ) στη μορφή
) στη μορφή 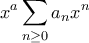 με
με  .
. ![\displaystyle{(a^2-2a)a_{0}x^{a-2}+(a^2-1)a_{1}x^{a-1}+(\color{red}a^2+2a\color{black})a_{2}x^a+\sum_{n\geq0}\left[\left(n^2+(4+2a)n+a^2+4a+3\right)a_{n+3}+4a_{n}\right]x^{n+a+1}=0} \displaystyle{(a^2-2a)a_{0}x^{a-2}+(a^2-1)a_{1}x^{a-1}+(\color{red}a^2+2a\color{black})a_{2}x^a+\sum_{n\geq0}\left[\left(n^2+(4+2a)n+a^2+4a+3\right)a_{n+3}+4a_{n}\right]x^{n+a+1}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/7ee82ab7fcf50802a1692ec25394af66.png)
 ή
ή 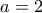 .
.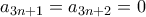 για
για  και
και  για
για  .
.
![\displaystyle{(a^2-2a)a_{0}x^{a-2}+(a^2-1)a_{1}x^{a-1}+(a^2+3a-2)a_{2}x^a+\sum_{n\geq0}\left[\left(n^2+(4+2a)n+a^2+4a+3\right)a_{n+3}+4a_{n}\right]x^{n+a+1}=0} \displaystyle{(a^2-2a)a_{0}x^{a-2}+(a^2-1)a_{1}x^{a-1}+(a^2+3a-2)a_{2}x^a+\sum_{n\geq0}\left[\left(n^2+(4+2a)n+a^2+4a+3\right)a_{n+3}+4a_{n}\right]x^{n+a+1}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/94dab6af9514a85ea2708ece025f6243.png)
 και το
και το  .Όταν λέτε στο δίκτυο υποθέτω εννοείται στο γνωστό άγνωστο site με τα πολλά βιβλία.
.Όταν λέτε στο δίκτυο υποθέτω εννοείται στο γνωστό άγνωστο site με τα πολλά βιβλία.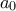 δηλαδή
δηλαδή 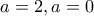 διαφέρουν κατά ακέραιο τρόπο ότι προκύπτει με ειδική παραγώγιση.
διαφέρουν κατά ακέραιο τρόπο ότι προκύπτει με ειδική παραγώγιση.

![a_{n+3}=\dfrac{-4a_{n}}{(n+r+3)(n+r+1)},\ a_1=a_2=0\xrightarrow[r=0]{n+3=3k}\\
a_{3k}=\dfrac{-4a_{3(k-1)}}{(3k)(3k-2)} a_{n+3}=\dfrac{-4a_{n}}{(n+r+3)(n+r+1)},\ a_1=a_2=0\xrightarrow[r=0]{n+3=3k}\\
a_{3k}=\dfrac{-4a_{3(k-1)}}{(3k)(3k-2)}](/forum/ext/geomar/texintegr/latexrender/pictures/bccf8646b4a6ec2e881933c480181dd0.png)