 με
με  . Να αποδείξετε πώς
. Να αποδείξετε πώς  και
και 
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

 τότε υπάρχει και το δεύτερο και είναι
τότε υπάρχει και το δεύτερο και είναι  . Απόδειξη: αν προσθέσουμε τις δύο ανάγεται στο
. Απόδειξη: αν προσθέσουμε τις δύο ανάγεται στο  που, ως γνωστόν, ισχύει.
που, ως γνωστόν, ισχύει. (για οποιαδήποτε ακολουθία). Απλά έγραψα την σταθερή ακολουθία διότι γι' αυτήν είναι προφανές ότι τα όρια είναι
(για οποιαδήποτε ακολουθία). Απλά έγραψα την σταθερή ακολουθία διότι γι' αυτήν είναι προφανές ότι τα όρια είναι  . Μάλλον κάτι άλλο θα ήθελε να ρωτήσει ο Νεγρεπόντης.
. Μάλλον κάτι άλλο θα ήθελε να ρωτήσει ο Νεγρεπόντης. και
και  τότε έχουμε
τότε έχουμε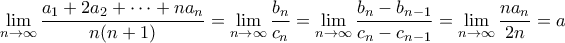 .
. .
.Συμφωνώ με το Δημήτρη ότι και τα δυο όρια είναιDemetres έγραψε:Νομίζω και τα δυο όρια βγαίνουν. Μάλλον κάτι άλλο θα ήθελε να ρωτήσει ο Νεγρεπόντης.
 .
.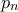 θετικοί και
θετικοί και  , τότε
, τότε  , από όπου και το αντίστοιχο δεύτερο όριο.
, από όπου και το αντίστοιχο δεύτερο όριο. 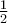 του
του 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες