Ακολουθία (8)
Δημοσιεύτηκε: Δευ Φεβ 14, 2011 3:40 pm
Δίνεται ακολουθία  , τέτοια ώστε
, τέτοια ώστε  και
και  .
.
Να υπολογιστεί το όριο
 , τέτοια ώστε
, τέτοια ώστε  και
και  .
.Να υπολογιστεί το όριο

 , τέτοια ώστε
, τέτοια ώστε  και
και  .
.
 τότε
τότε 
 . Τότε
. Τότε 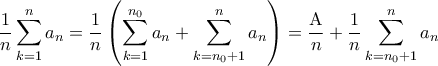
 .
. προκύπτει ότι
προκύπτει ότι  .
.  . Ορίζουμε
. Ορίζουμε  , τότε
, τότε  . Η ακολουθία
. Η ακολουθία  είναι (φανερά) γνησίως αύξουσα και μη φραγμένη, διότι
είναι (φανερά) γνησίως αύξουσα και μη φραγμένη, διότι 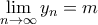 . Τότε
. Τότε  που είναι αδύνατο.
που είναι αδύνατο. .
.  .
. είναι θετικών όρων.
είναι θετικών όρων.  (1)
(1) .
.  είναι γνησίως φθίνουσα και φραγμένη κάτω, άρα συγκλίνει.
είναι γνησίως φθίνουσα και φραγμένη κάτω, άρα συγκλίνει.
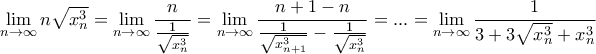

 , και βλέπουμε έυκολα ότι η
, και βλέπουμε έυκολα ότι η  είναι γνησίως αύξουσα και
είναι γνησίως αύξουσα και  .
.![\displaystyle{y_{n+1}^3-y_{n}^3=\left(y_{n}+\frac{1}{y_{n}^2}\right)^3-y_{n}^3=y_{n}^3\left[\left(1+\frac{1}{y_{n}^3}\right)^3-1\right]\stackrel{(1+x)^a=1+ax+o(x),\,|x|<1}{=}y_{n}^3\left(1+\frac{3}{y_{n}^3}+o(1/y_{n}^3)-1\right)=3+o(1)\to3\qquad\boxed{1}} \displaystyle{y_{n+1}^3-y_{n}^3=\left(y_{n}+\frac{1}{y_{n}^2}\right)^3-y_{n}^3=y_{n}^3\left[\left(1+\frac{1}{y_{n}^3}\right)^3-1\right]\stackrel{(1+x)^a=1+ax+o(x),\,|x|<1}{=}y_{n}^3\left(1+\frac{3}{y_{n}^3}+o(1/y_{n}^3)-1\right)=3+o(1)\to3\qquad\boxed{1}}](/forum/ext/geomar/texintegr/latexrender/pictures/e32f6dd3da7df54c47ab634c0dcca83d.png) .
. , άρα
, άρα  .
. στην
στην  , γράφοντας δηλαδή
, γράφοντας δηλαδή  , έχουμε
, έχουμε .
. ,
,  έχουν σταθερό πρόσημο,
έχουν σταθερό πρόσημο,  και μια από τις δυο αντίστοιχες σειρές αποκλίνει, τότε
και μια από τις δυο αντίστοιχες σειρές αποκλίνει, τότε  .
. , άρα
, άρα  , καθώς
, καθώς  .
. , άρα
, άρα .
.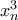 , παίρνουμε το ζητούμενο όριο καθώς επίσης και ότι
, παίρνουμε το ζητούμενο όριο καθώς επίσης και ότι , το οποίο παρουσϊαζε απροσδιοριστία.
, το οποίο παρουσϊαζε απροσδιοριστία. με όση ακρίβεια θέλουμε.
με όση ακρίβεια θέλουμε.