 με
με 
συγκλίνει ομοιόμορφα.
ΣΗΜΕΙΩΣΗ: Δεν έχω λύση. Όμως, επειδή την κοίταξα αρκετά, έχω πεισθεί ότι συγκλίνει ομοιόμορφα.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 με
με 

Είναι απλό να δούμε ότι η ακολουθία συγκλίνει κατά σημείο στην

 ,
, 

 τέτοια, ώστε
τέτοια, ώστε 
 , όπου θέσαμε
, όπου θέσαμε 
 και παραγωγίζοντας δύο φορές βρίσκουμε
και παραγωγίζοντας δύο φορές βρίσκουμε 
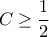 έχουμε
έχουμε 
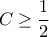 έχουμε
έχουμε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες