Δίνουμε μια λύση της άσκησης:
i. Ένα κάθετο διάνυσμα της επιφάνειας

στο σημείο

- σημείο που βρίσκεται και επί της περιφέρειας
![C:\big(\frac{5}{4}\cos{t},\frac{5}{4}\sin{t},\log\big(\frac{3}{4}\big)\big)\,,\; t\in[0,2\pi] C:\big(\frac{5}{4}\cos{t},\frac{5}{4}\sin{t},\log\big(\frac{3}{4}\big)\big)\,,\; t\in[0,2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/08d12269e5b3feb488d965b5b4d11865.png)
- είναι το


- iscr1.png (83.87 KiB) Προβλήθηκε 397 φορές
Επομένως η ευθεία

διέρχεται από το κέντρο της ζητούμενης σφαίρας

. Επειδή το κέντρο της σφαίρας βρίσκεται επί του

-άξονα, πρέπει

Επομένως το κέντρο είναι το σημείο

.
Η ακτίνα της ζητούμενης σφαίρας ισούται με

Τελικά η εξίσωση της σφαίρας είναι
 ii.
ii. Το στερεό
περικλείεται από την επιφάνεια -που παράγεται από την περιστροφή της καμπύλης

περί τον

-άξονα- και το επίπεδο

.

- iscr2.png (73.41 KiB) Προβλήθηκε 397 φορές
Το τμήμα

έχει παραμετρική παράσταση
![\displaystyle \overline{c}_1(t)=\big(\cosh{t},0,\log(\sinh{t})\big)\,,\; t\in\big[\sinh^{-1}\big(\tfrac{1}{7}\big),\sinh^{-1}\big(\tfrac{3}{4}\big)\big]\,. \displaystyle \overline{c}_1(t)=\big(\cosh{t},0,\log(\sinh{t})\big)\,,\; t\in\big[\sinh^{-1}\big(\tfrac{1}{7}\big),\sinh^{-1}\big(\tfrac{3}{4}\big)\big]\,.](/forum/ext/geomar/texintegr/latexrender/pictures/7c2076b4eb825173d0fef5cc861553bc.png)
Για το τμήμα

, αρκεί να προσδιοριστεί η γωνία

. Από το ορθογώνιο τρίγωνο

έχουμε ότι

και, επομένως, μια παραμετρική παράσταση του τμήματος

είναι
![\displaystyle \overline{c}_2(t)=\big(\tfrac{\sqrt{481}}{16}\sin{t},0,\log\big(\tfrac{3}{4}\big)+\tfrac{9}{16}-\tfrac{\sqrt{481}}{16}\cos{t}\big)\,,\; t\in\big[\arccos\big(\tfrac{9}{\sqrt{481}}\big),\pi\big]\,. \displaystyle \overline{c}_2(t)=\big(\tfrac{\sqrt{481}}{16}\sin{t},0,\log\big(\tfrac{3}{4}\big)+\tfrac{9}{16}-\tfrac{\sqrt{481}}{16}\cos{t}\big)\,,\; t\in\big[\arccos\big(\tfrac{9}{\sqrt{481}}\big),\pi\big]\,.](/forum/ext/geomar/texintegr/latexrender/pictures/29b690b4abe32310f8c62d6ba8e636b1.png)
Ο όγκος του στερεού

που "παράγεται" από την περιστροφή της
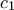
ισούται με
![\begin{aligned}
V(\Sigma_1)&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\cosh^2{t}\,\frac{d}{dt}\log(\sinh{t})\,dt\\\noalign{\vspace{0.2cm}}
&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\frac{\cosh^3{t}}{\sinh{t}}\,dt\\\noalign{\vspace{0.2cm}}
&\mathop{=\!=\!=\!=\!=\!=\!=}\limits^{{\begin{subarray}{c}
{u\,=\,\sinh{t}} \\\noalign{\vspace{0.05cm}}
{du\,=\,\cosh{t}\,dt} \\\noalign{\vspace{0.05cm}}
\end{subarray}}}\,\pi\int_{\frac{1}{7}}^{\frac{3}{4}}\frac{1+u^2}{u}\,du\\\noalign{\vspace{0.2cm}}
&=\pi\bigg[\log{u}+\frac{u^2}{2}\bigg]_{\frac{1}{7}}^{\frac{3}{4}}\\\noalign{\vspace{0.2cm}}
&=\pi\Big(\log\big(\tfrac{3}{4}\big)+\log{7}+\frac{425}{1568}\Big)\,.
\end{aligned} \begin{aligned}
V(\Sigma_1)&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\cosh^2{t}\,\frac{d}{dt}\log(\sinh{t})\,dt\\\noalign{\vspace{0.2cm}}
&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\frac{\cosh^3{t}}{\sinh{t}}\,dt\\\noalign{\vspace{0.2cm}}
&\mathop{=\!=\!=\!=\!=\!=\!=}\limits^{{\begin{subarray}{c}
{u\,=\,\sinh{t}} \\\noalign{\vspace{0.05cm}}
{du\,=\,\cosh{t}\,dt} \\\noalign{\vspace{0.05cm}}
\end{subarray}}}\,\pi\int_{\frac{1}{7}}^{\frac{3}{4}}\frac{1+u^2}{u}\,du\\\noalign{\vspace{0.2cm}}
&=\pi\bigg[\log{u}+\frac{u^2}{2}\bigg]_{\frac{1}{7}}^{\frac{3}{4}}\\\noalign{\vspace{0.2cm}}
&=\pi\Big(\log\big(\tfrac{3}{4}\big)+\log{7}+\frac{425}{1568}\Big)\,.
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/4f1b092c66b839a937bfade5053cf68d.png)
Ο όγκος του στερεού

που "παράγεται" από την περιστροφή της

ισούται με

Άρα

 η επιφάνεια εκ περιστροφής με παραμετρική παράσταση
η επιφάνεια εκ περιστροφής με παραμετρική παράσταση
![\displaystyle {\bf{X}}:(0,1]\times[0,2\pi]\longrightarrow\mathbb{R}^3\,;\; {\bf{X}}(u,v)=\begin{pmatrix}
\cosh{u}\cos{v}\\
\cosh{u}\sin{v}\\
\log(\sinh{u})
\end{pmatrix}\,. \displaystyle {\bf{X}}:(0,1]\times[0,2\pi]\longrightarrow\mathbb{R}^3\,;\; {\bf{X}}(u,v)=\begin{pmatrix}
\cosh{u}\cos{v}\\
\cosh{u}\sin{v}\\
\log(\sinh{u})
\end{pmatrix}\,.](/forum/ext/geomar/texintegr/latexrender/pictures/8a002998fb0d0fe7dc43a5cd2f39144c.png)
 που έχει κέντρο επί του
που έχει κέντρο επί του  -άξονα και εφάπτεται της
-άξονα και εφάπτεται της  κατά μήκος της περιφέρειας
κατά μήκος της περιφέρειας ![C:\big(\frac{5}{4}\cos{t},\frac{5}{4}\sin{t},\log\big(\frac{3}{4}\big)\big)\,,\; t\in[0,2\pi] C:\big(\frac{5}{4}\cos{t},\frac{5}{4}\sin{t},\log\big(\frac{3}{4}\big)\big)\,,\; t\in[0,2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/08d12269e5b3feb488d965b5b4d11865.png) .
. που περικλείεται από:
που περικλείεται από:
 που βρίσκεται "πάνω" από την περιφέρεια
που βρίσκεται "πάνω" από την περιφέρεια  ,
, που βρίσκεται "κάτω" από την περιφέρεια
που βρίσκεται "κάτω" από την περιφέρεια  και
και .
.

 του επιπέδου
του επιπέδου  , το κέντρο και την ακτίνα του
, το κέντρο και την ακτίνα του  , το σημείο
, το σημείο  στο οποίο η καμπύλη αυτή συναντά τον κύκλο αυτό, καθώς και την
στο οποίο η καμπύλη αυτή συναντά τον κύκλο αυτό, καθώς και την  της καμπύλης αυτής η οποία θα δώσει και το κέντρο
της καμπύλης αυτής η οποία θα δώσει και το κέντρο  της ζητούμενης σφαίρας.
της ζητούμενης σφαίρας. - σημείο που βρίσκεται και επί της περιφέρειας
- σημείο που βρίσκεται και επί της περιφέρειας 
 διέρχεται από το κέντρο της ζητούμενης σφαίρας
διέρχεται από το κέντρο της ζητούμενης σφαίρας 
 .
. 

 περί τον
περί τον  .
.
 έχει παραμετρική παράσταση
έχει παραμετρική παράσταση ![\displaystyle \overline{c}_1(t)=\big(\cosh{t},0,\log(\sinh{t})\big)\,,\; t\in\big[\sinh^{-1}\big(\tfrac{1}{7}\big),\sinh^{-1}\big(\tfrac{3}{4}\big)\big]\,. \displaystyle \overline{c}_1(t)=\big(\cosh{t},0,\log(\sinh{t})\big)\,,\; t\in\big[\sinh^{-1}\big(\tfrac{1}{7}\big),\sinh^{-1}\big(\tfrac{3}{4}\big)\big]\,.](/forum/ext/geomar/texintegr/latexrender/pictures/7c2076b4eb825173d0fef5cc861553bc.png)
 , αρκεί να προσδιοριστεί η γωνία
, αρκεί να προσδιοριστεί η γωνία  . Από το ορθογώνιο τρίγωνο
. Από το ορθογώνιο τρίγωνο  έχουμε ότι
έχουμε ότι  και, επομένως, μια παραμετρική παράσταση του τμήματος
και, επομένως, μια παραμετρική παράσταση του τμήματος ![\displaystyle \overline{c}_2(t)=\big(\tfrac{\sqrt{481}}{16}\sin{t},0,\log\big(\tfrac{3}{4}\big)+\tfrac{9}{16}-\tfrac{\sqrt{481}}{16}\cos{t}\big)\,,\; t\in\big[\arccos\big(\tfrac{9}{\sqrt{481}}\big),\pi\big]\,. \displaystyle \overline{c}_2(t)=\big(\tfrac{\sqrt{481}}{16}\sin{t},0,\log\big(\tfrac{3}{4}\big)+\tfrac{9}{16}-\tfrac{\sqrt{481}}{16}\cos{t}\big)\,,\; t\in\big[\arccos\big(\tfrac{9}{\sqrt{481}}\big),\pi\big]\,.](/forum/ext/geomar/texintegr/latexrender/pictures/29b690b4abe32310f8c62d6ba8e636b1.png)
 που "παράγεται" από την περιστροφή της
που "παράγεται" από την περιστροφή της 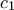 ισούται με
ισούται με ![\begin{aligned}
V(\Sigma_1)&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\cosh^2{t}\,\frac{d}{dt}\log(\sinh{t})\,dt\\\noalign{\vspace{0.2cm}}
&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\frac{\cosh^3{t}}{\sinh{t}}\,dt\\\noalign{\vspace{0.2cm}}
&\mathop{=\!=\!=\!=\!=\!=\!=}\limits^{{\begin{subarray}{c}
{u\,=\,\sinh{t}} \\\noalign{\vspace{0.05cm}}
{du\,=\,\cosh{t}\,dt} \\\noalign{\vspace{0.05cm}}
\end{subarray}}}\,\pi\int_{\frac{1}{7}}^{\frac{3}{4}}\frac{1+u^2}{u}\,du\\\noalign{\vspace{0.2cm}}
&=\pi\bigg[\log{u}+\frac{u^2}{2}\bigg]_{\frac{1}{7}}^{\frac{3}{4}}\\\noalign{\vspace{0.2cm}}
&=\pi\Big(\log\big(\tfrac{3}{4}\big)+\log{7}+\frac{425}{1568}\Big)\,.
\end{aligned} \begin{aligned}
V(\Sigma_1)&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\cosh^2{t}\,\frac{d}{dt}\log(\sinh{t})\,dt\\\noalign{\vspace{0.2cm}}
&=\pi\int_{\sinh^{-1}(\frac{1}{7})}^{\sinh^{-1}(\frac{3}{4})}\frac{\cosh^3{t}}{\sinh{t}}\,dt\\\noalign{\vspace{0.2cm}}
&\mathop{=\!=\!=\!=\!=\!=\!=}\limits^{{\begin{subarray}{c}
{u\,=\,\sinh{t}} \\\noalign{\vspace{0.05cm}}
{du\,=\,\cosh{t}\,dt} \\\noalign{\vspace{0.05cm}}
\end{subarray}}}\,\pi\int_{\frac{1}{7}}^{\frac{3}{4}}\frac{1+u^2}{u}\,du\\\noalign{\vspace{0.2cm}}
&=\pi\bigg[\log{u}+\frac{u^2}{2}\bigg]_{\frac{1}{7}}^{\frac{3}{4}}\\\noalign{\vspace{0.2cm}}
&=\pi\Big(\log\big(\tfrac{3}{4}\big)+\log{7}+\frac{425}{1568}\Big)\,.
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/4f1b092c66b839a937bfade5053cf68d.png)
 που "παράγεται" από την περιστροφή της
που "παράγεται" από την περιστροφή της  ισούται με
ισούται με 
