george visvikis έγραψε: ↑Πέμ Ιαν 27, 2022 12:56 pm
Ο καθηγητής των μαθηματικών μπαίνει σε ένα τμήμα της α' λυκείου και γράφει στον πίνακα:
Αν

και

θα αποδείξουμε ότι

Στη συνέχεια από τη δοσμένη σχέση αναπτύσσοντας την ταυτότητα βρίσκει


Τέλος γράφει,

"Το καταλάβατε;" ρωτάει.
"Μάλιστα," απαντούν εν χορώ οι μαθητές και οι μαθήτριες.
"Μήπως βλέπετε κάποιο λάθος;" ρωτάει και πάλι ο καθηγητής.
Τα παιδιά κοιτούν τον πίνακα με απορία. Σε κάποια στιγμή ένας μαθητής, ο
Εξυπνούλης, σηκώνει το χέρι του και λέει τη γνώμη του. "Μπράβο,
Εξυπνούλη, παιδί μου!" του απαντά ο καθηγητής με θαυμασμό.
Τι είδε ο
Εξυπνούλης που δεν είδαν οι συμμαθητές και οι συμμαθήτριές του;
24 ώρες για μαθητές.
Πιθανόν ο Εξυπνούλης να μην είδε το λάθος στην αρχική ισότητα (γιατί είναι και λίγο κρυμμένο) . Μπορεί να μην είδε το λάθος στην

αλλά στην απόδειξη ότι

πιθανόν να διερωτήθηκε για ποια τιμή του

ισχύει (και θα ήταν και σοφό από την μεριά του για επιβεβαίωση της απάντησης του ).
Έτσι κάνοντας απαλοιφή στην πιο πάνω σχέση (προσπαθώντας να βρει το

) θα κατέληγε ότι

οπότε τι σκέφτεται ένας εξυπνούλης (αλλά παιδί ! ) που γνωρίζει ότι κάθε άρτια δύναμη πραγματικού αριθμού είναι μη αρνητικός αριθμός;
Το πρώτο πράγμα που έρχεται στο μυαλό του είναι ότι έχει κάνει λάθος.
Αλλά ποιο είναι το λάθος;
Είναι λογικό ή είναι λογιστικό;
Επειδή όμως είναι άριστος στις πράξεις και γνωρίζει και τις ταυτότητες πολύ καλά
Το ξανακοιτάει , το ξανακοιτάει και δεν βρίσκει λάθος. Είναι όμως βέβαιος ότι το αποτέλεσμα δεν είναι σωστό .
Έχετε απάντηση για την ψυχολογική του κατάσταση ;
Έχει τα «κουράγια» να το «προσπεράσει» ή θα το σβήσει αφού δεν θα βρει ποτέ το «λάθος» ΤΟΥ;
Θα συμφωνήσω λοιπόν με το Βασίλη ότι τέτοιου είδους θέματα δεν είναι για μαθητές και θα συμφωνήσω για το «Μπράβο» που του είπε ο Καθηγητής του εννοείται για την παρατηρητικότητά του !!!
 και
και  θα αποδείξουμε ότι
θα αποδείξουμε ότι 




 και
και  ) Κάνει τουλάχιστον
) Κάνει τουλάχιστον  και προφανώς όλα όσα βρήκε ειναι λανθασμένα ( δεν υπαρχει πραγματικός αριθμός
και προφανώς όλα όσα βρήκε ειναι λανθασμένα ( δεν υπαρχει πραγματικός αριθμός  για τον οποίο να ισχύουν )
για τον οποίο να ισχύουν )
 για θετικά, ανάλογα για αρνητικά, και λοιπά. Άλλος τρόπος είναι να λύσουμε την εξίσωση, οπότε θα βρούμε (μιγαδικές) ρίζες
για θετικά, ανάλογα για αρνητικά, και λοιπά. Άλλος τρόπος είναι να λύσουμε την εξίσωση, οπότε θα βρούμε (μιγαδικές) ρίζες  . Οπότε "δεν μας εκπλήσει" αν βρούμε ότι
. Οπότε "δεν μας εκπλήσει" αν βρούμε ότι  . Μπορούμε βέβαια να το επαληθεύσουμε κάνοντας τις πράξεις. Ακόμα καλύτερα, μπορούμε να πάμε με τους πάλαι ποτέ τύπους της Τριγωνομετρικής μορφής μιγαδικών και να θυμηθούμε τον De Moivre (οι πολύύύ παλιοί ξέρουν τι εννοώ).
. Μπορούμε βέβαια να το επαληθεύσουμε κάνοντας τις πράξεις. Ακόμα καλύτερα, μπορούμε να πάμε με τους πάλαι ποτέ τύπους της Τριγωνομετρικής μορφής μιγαδικών και να θυμηθούμε τον De Moivre (οι πολύύύ παλιοί ξέρουν τι εννοώ). , οπότε
, οπότε  και
και  .
. 

 αλλά στην απόδειξη ότι
αλλά στην απόδειξη ότι  πιθανόν να διερωτήθηκε για ποια τιμή του
πιθανόν να διερωτήθηκε για ποια τιμή του  ισχύει (και θα ήταν και σοφό από την μεριά του για επιβεβαίωση της απάντησης του ).
ισχύει (και θα ήταν και σοφό από την μεριά του για επιβεβαίωση της απάντησης του ).  οπότε τι σκέφτεται ένας εξυπνούλης (αλλά παιδί ! ) που γνωρίζει ότι κάθε άρτια δύναμη πραγματικού αριθμού είναι μη αρνητικός αριθμός;
οπότε τι σκέφτεται ένας εξυπνούλης (αλλά παιδί ! ) που γνωρίζει ότι κάθε άρτια δύναμη πραγματικού αριθμού είναι μη αρνητικός αριθμός; είναι ομόσημοι, οπότε δεν μπορεί να έχουν άθροισμα
είναι ομόσημοι, οπότε δεν μπορεί να έχουν άθροισμα 
 ή
ή  άρα δεν μπορεί να είναι
άρα δεν μπορεί να είναι  "
" ή
ή 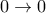 ;
;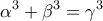 και
και  να δείξετε ότι οι
να δείξετε ότι οι ![\displaystyle \alpha ,\gamma ,\beta \sqrt[3]{4} \displaystyle \alpha ,\gamma ,\beta \sqrt[3]{4}](/forum/ext/geomar/texintegr/latexrender/pictures/14128c8dcd569f78d36c57963075d6ee.png) είναι διαδοχικοί όροι γεωμετρικής προόδου.
είναι διαδοχικοί όροι γεωμετρικής προόδου.