Καλησπέρα σε όλους. Ευχαριστώ τον
Μανώλη και τον
Γιώργο για τις απαντήσεις τους.
Έφερα στη μνήμη μου το θέμα, επειδή (αναζητώντας κάτι άλλο) συνάντησα στο τεύχος 90 του Ευκλείδη Γ΄(2019) το πολύ ενδιαφέρον άρθρο των
Κώστα Δόρτσιου και
Δημήτρη Ντρίζου, με τίτλο
Από τις “διαισθητικές προσεγγίσεις” στις “μαθηματικές βεβαιότητες”, όπου διερευνάται σε βάθος το θέμα.
Ας δώσω μια παραλλαγή των όμορφων αποδείξεων του
Γιώργου και του
Μανώλη:
Ορθόν:

- 27-12-2020 Γεωμετρία.png (12.02 KiB) Προβλήθηκε 830 φορές

Αφού

, είναι

,
οπότε το

ανήκει στο τμήμα

και στο τρίγωνο

η διάμεσος

ισούται με το μισό της

, άρα είναι ορθογώνιο, οπότε ισχύει
 Αντίστροφον:
Αντίστροφον:

- 27-12-2020 Γεωμετρία c.png (12.55 KiB) Προβλήθηκε 830 φορές
Έστω τρίγωνο

με πλευρές

, για το οποίο ισχύει

, άρα είναι ορθογώνιο με υποτείνουσα τη

.
Τότε η διάμεσος

το χωρίζει σε δύο ισεμβαδικά τρίγωνα

με πλευρές

αντίστοιχα.
 , ενώ το δεύτερο
, ενώ το δεύτερο  .
.
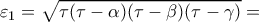 \sqrt{169(169-109)(169-109)(169-120)}
\sqrt{169(169-109)(169-109)(169-120)}
 η ημιπερίμετρος του τριγώνου και
η ημιπερίμετρος του τριγώνου και  τα μήκη των πλευρών του τριγώνου.Για το εμβαδόν του δεύτερου τριγώνου έχουμε:
τα μήκη των πλευρών του τριγώνου.Για το εμβαδόν του δεύτερου τριγώνου έχουμε: \sqrt{200(200-109)(200-109)(200-182)}
\sqrt{200(200-109)(200-109)(200-182)} .
.  και οι διαδοχικές πλευρές ίσες που δίνει ότι έχουν ίσα εμβαδά.
και οι διαδοχικές πλευρές ίσες που δίνει ότι έχουν ίσα εμβαδά.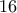 άχρονος ; ) και τον
άχρονος ; ) και τον 
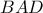 και
και  με πλευρές
με πλευρές  και
και  είναι ισεμβαδικά.
είναι ισεμβαδικά.
 και
και  .. Φιλικά, Γιώργος.
.. Φιλικά, Γιώργος. , οπότε τα τρίγωνα
, οπότε τα τρίγωνα  Γενίκευση.
Γενίκευση. και
και  με
με  είναι ισεμβαδικά ανν
είναι ισεμβαδικά ανν  .
.







 , είναι
, είναι  ,
, ανήκει στο τμήμα
ανήκει στο τμήμα  και στο τρίγωνο
και στο τρίγωνο  η διάμεσος
η διάμεσος  ισούται με το μισό της
ισούται με το μισό της 
 , για το οποίο ισχύει
, για το οποίο ισχύει  με πλευρές
με πλευρές  αντίστοιχα.
αντίστοιχα. . Θεωρούμε το (ορθογώνιο ) τρίγωνο-
. Θεωρούμε το (ορθογώνιο ) τρίγωνο-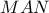 με πλευρές
με πλευρές 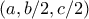 . Με συμμετρίες σχηματίζουμε τα τρίγωνα:
. Με συμμετρίες σχηματίζουμε τα τρίγωνα:  με πλευρές
με πλευρές  και
και  με πλευρές
με πλευρές  .
.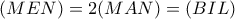 .
.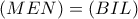 .
. και με
και με 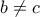 προκύπτει
προκύπτει  .
.  ύψη έχουμε
ύψη έχουμε  οπότε τα ορθ. τρίγωνα
οπότε τα ορθ. τρίγωνα 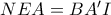 είναι ίσα και ευκολα παίρνουμε
είναι ίσα και ευκολα παίρνουμε  . Φιλικά, Γιώργος.
. Φιλικά, Γιώργος.