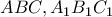 έχουν διαμέσους
έχουν διαμέσους  αντίστοιχα και
αντίστοιχα και 
Είναι τα τρίγωνα αυτά όμοια; Αιτιολογήστε την απάντησή σας.
Μέχρι 18/07/2018
Συντονιστής: polysot
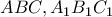 έχουν διαμέσους
έχουν διαμέσους  αντίστοιχα και
αντίστοιχα και 
 και
και 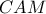 . Έχουμε:
. Έχουμε: και
και  .
.  και
και  , αφού οι γωνίες αυτές είναι παραπληρωματικές, έχουμε ότι
, αφού οι γωνίες αυτές είναι παραπληρωματικές, έχουμε ότι 
 και
και  και προκύπτει ότι:
και προκύπτει ότι:
 , άρα αφού
, άρα αφού  , τα τρίγωνα είναι πράγματι όμοια.
, τα τρίγωνα είναι πράγματι όμοια.Ανgeorge visvikis έγραψε: ↑Δευ Ιούλ 16, 2018 7:26 pmΚριτήριο ομοιότητας.png
Τα τρίγωναέχουν διαμέσους
αντίστοιχα και

Είναι τα τρίγωνα αυτά όμοια; Αιτιολογήστε την απάντησή σας.
Μέχρι 18/07/2018
 τα συμμετρικά των
τα συμμετρικά των  ως προς τα
ως προς τα 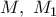 αντίστοιχα , τότε αβίαστα προκύπτουν:
αντίστοιχα , τότε αβίαστα προκύπτουν:  είναι παραλληλόγραμμα .
είναι παραλληλόγραμμα .  είναι όμοια .
είναι όμοια .  συνεπώς τα τρίγωνα
συνεπώς τα τρίγωνα 
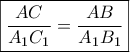 . και τις περιεχόμενες γωνίες ,
. και τις περιεχόμενες γωνίες , 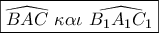 ίσες, οπότε είναι όμοια .
ίσες, οπότε είναι όμοια .Παίρνω τοgeorge visvikis έγραψε: ↑Δευ Ιούλ 16, 2018 7:26 pmΚριτήριο ομοιότητας.png
Τα τρίγωναέχουν διαμέσους
αντίστοιχα και

Είναι τα τρίγωνα αυτά όμοια; Αιτιολογήστε την απάντησή σας.
Μέχρι 18/07/2018
 και το τοποθετώ πάνω στο
και το τοποθετώ πάνω στο 
 θα πέσει πάνω στην
θα πέσει πάνω στην 
 είναι παράλληλη στην
είναι παράλληλη στην  τέλος.
τέλος. που περνάει από το
που περνάει από το  και είναι παράλληλη στην
και είναι παράλληλη στην  .
. παραλληλόγραμμο ΑΤΟΠΟ
παραλληλόγραμμο ΑΤΟΠΟ ισχύει επιπλέον
ισχύει επιπλέον  να εξεταστεί αν αυτά είναι όμοια
να εξεταστεί αν αυτά είναι όμοια :
:  . Ομοίως στο
. Ομοίως στο 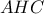 :
:  .
. 
 προκύπτουν
προκύπτουν  και
και 

 παίρνουμε
παίρνουμε  ενώ
ενώ  που σημαίνει ότι τα εν λόγω τρίγωνα είναι όμοια.. Φιλικά Γιώργος.
που σημαίνει ότι τα εν λόγω τρίγωνα είναι όμοια.. Φιλικά Γιώργος. θεωρώ τα σημεία
θεωρώ τα σημεία  αντίστοιχα, ώστε
αντίστοιχα, ώστε  Άρα τα τρίγωνα
Άρα τα τρίγωνα  είναι ίσα και το
είναι ίσα και το  που είναι αντίστοιχο του
που είναι αντίστοιχο του  θα πέσει πάνω στην
θα πέσει πάνω στην 
 και το ζητούμενο έπεται.
και το ζητούμενο έπεται. επαρκώς για να συμπέσουν
επαρκώς για να συμπέσουν 
 .Εύκολα βλέπουμε ότι δεδομένου ότι βρίσκονται τα 2 τρίγωνα στο ίδιο ημιεπίπεδο,το
.Εύκολα βλέπουμε ότι δεδομένου ότι βρίσκονται τα 2 τρίγωνα στο ίδιο ημιεπίπεδο,το  βρίσκεται πάνω σε κύκλους που ορίζονται από τα
βρίσκεται πάνω σε κύκλους που ορίζονται από τα  ,δηλαδή είναι η τομή τους,το
,δηλαδή είναι η τομή τους,το  κλπ.
κλπ.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες