 είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  , τριγώνου
, τριγώνου  , ενώ το
, ενώ το 
είναι το μέσο της
 . Στην προέκταση της
. Στην προέκταση της  κινείται σημείο
κινείται σημείο  και οι
και οι 
τέμνουν την πλευρά
 , στα σημεία
, στα σημεία  αντίστοιχα . Υπολογίστε το λόγο :
αντίστοιχα . Υπολογίστε το λόγο : 
Ε ! πριν έλθει το Σαββατοκύριακο .
Συντονιστής: polysot
 είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  , τριγώνου
, τριγώνου  , ενώ το
, ενώ το 
 . Στην προέκταση της
. Στην προέκταση της  κινείται σημείο
κινείται σημείο  και οι
και οι 
 , στα σημεία
, στα σημεία  αντίστοιχα . Υπολογίστε το λόγο :
αντίστοιχα . Υπολογίστε το λόγο : 
 τέμνει την
τέμνει την  στο
στο  .
.  και έστω
και έστω  το σημείο τομής της με την
το σημείο τομής της με την  .
.  και
και  και τις παράλληλες
και τις παράλληλες  και
και  προκύπτει ότι:
προκύπτει ότι:
 είναι το βαρύκεντρο του
είναι το βαρύκεντρο του  ,συνεπώς ισχύει ότι:
,συνεπώς ισχύει ότι:  (1)
(1)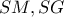 και
και  και τις παράλληλες
και τις παράλληλες  και
και  , προκύπτει ότι:
, προκύπτει ότι: 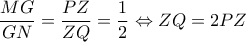 (2)
(2)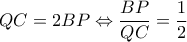
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες