θεώρημα γλαφυρόν...

[gbaloglou]

[Ανάπτυγμα της δεκάλεπτης εισήγησης μου, επικεντρωμένης στις ενότητες 7.6-7.7 και 8.1-8.10 (βλέπε και συνημμένο), κατά την σημερινή παρουσίαση της ΙΣΤΟΡΙΑΣ ΑΡΧΑΙΩΝ ΕΛΛΗΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΩΝ (του Στέλιου Νεγρεπόντη και της Βασιλικής Φαρμάκη, Εκδόσεις Εκκρεμές) στην 16η Διεθνή Έκθεση Βιβλίου Θεσσαλονίκης.]

Μία από τις κύριες αρετές του βιβλίου είναι η δυνατότητα που δίνει στους σύγχρονους Έλληνες να 'νιώσουν' τις μαθηματικές δημιουργίες των προγόνων τους μέσα από την πολύ γενναιόδωρη παράθεση αρχαιοελληνικών κειμένων. Τα κείμενα αυτά δεν αποδίδονται πάντα στην νεοελληνική, η κατανόηση τους διευκολύνεται όμως από την συζήτηση των σχετικών με αυτά Μαθηματικών. Και ένα από τα ωραιότερα παρατιθέμενα κείμενα είναι η διατύπωση του Γλαφυρού Θεωρήματος από τον Πρόκλο (εις Πολιτείαν 2.27, 11-16).

Το θεώρημα που ο Πρόκλος ονομάζει "γλαφυρό", αρκετούς αιώνες μετά την ανακάλυψη του από τους Πυθαγόρειους, δεν είναι δύσκολο να αποδειχθεί με πολύ στοιχειώδη γεωμετρικό τρόπο. Αυτό φαίνεται και από την απόδειξη που παρατίθεται στην σελίδα 370, και από την απόδειξη που βρήκα κατά την πρώτη σοβαρή φυλλομέτρηση του βιβλίου στις 2-4-2019 (την ημέρα δηλαδή που μου έγινε, μάλλον απρόσμενα, η πρόταση παρουσίασης του βιβλίου ). Ο Πρόκλος πάντως το αποδεικνύει γεωμετρικά με χρήση της Πρότασης 2.10 των Στοιχείων (που στην αλγεβρική της μορφή είναι η ταυτότητα ): αν τότε (αλγεβρικοποιώντας την απόδειξη πάντοτε).

[Χρειάζεται προσοχή στο τι είναι/ήταν 'αλγεβρικό' και τι 'γεωμετρικό', και αυτό άπτεται του γενικότερου ερωτήματος αν είχαν όντως φθάσει οι Πυθαγόρειοι (και το Δεύτερο Βιβλίο των Στοιχείων) στην λεγόμενη Γεωμετρική Άλγεβρα, ένα από τα κύρια θέματα του βιβλίου που δεν θίγεται εδώ.]

Σε απλή νεοελληνική το γλαφυρό θεώρημα μας λέει ότι κάθε ισοσκελές ορθογώνιο τρίγωνο πλευράς και διαμέτρου (υποτείνουσας) μπορεί να 'επεκταθεί' σε ισοσκελές ορθογώνιο τρίγωνο πλευράς και διαμέτρου . Αυτή η 'επέκταση', , θα μπορούσε να μας δώσει την ιδέα για την δημιουργία δύο ακολουθιών που ορίζονται αναδρομικά από τους τύπους : αρχίζοντας 'για παράδειγμα' με , λαμβάνουμε , , , κλπ: αυτοί οι αριθμοί αποκαλούνται πλευρικοί και διαμετρικοί, αντίστοιχα.

Θεωρώντας ισοσκελή τρίγωνα βάσης και ίσων πλευρών παρατηρούμε ότι γρήγορα αυτά τείνουν προς ισοσκελές ορθογώνιο τρίγωνο διαμέτρου . Από μια κάπως διαφορετική σκοπιά, βλέπουμε ότι τα τρίγωνα {} είναι ότι πλησιέστερο μπορούμε να έχουμε σε ισοσκελή ορθογώνια τρίγωνα με ακέραιες πλευρές και ακέραια διάμετρο, καθώς ισχύει η 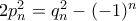. Σε σύγχρονη μαθηματική γλώσσα, θα λέγαμε ότι τα ζεύγη αποτελούν λύσεις της εξίσωσης Pell, ή ότι έχουν την ιδιότητα Pell.

Είχαν αποδείξει οι Πυθαγόρειοι την ιδιότητα Pell; Αυτό αποτελεί αντικείμενο διαμάχης ανάμεσα στους ειδικούς, όπως λεπτομερώς συζητούν οι συγγραφείς, που επιχειρηματολογούν, αρκετά πειστικά, υπέρ της αισιόδοξης άποψης: υποστηρίζουν συγκεκριμένα την χρήση κάποιας μορφής μαθηματικής επαγωγής με επαγωγικό βήμα βασιζόμενο στην 'Πυθαγόρεια' ισότητα ), που προκύπτει και αυτή από την Πρόταση 2.10 των Στοιχείων (και από τον αναδρομικό ορισμό των δύο ακολουθιών). [Η κρίσιμη αυτή ισότητα είχε, όπως επισημαίνουν οι συγγραφείς, διαφύγει της προσοχής του διάσημου ιστορικού των Μαθηματικών David Fowler, που τάραξε τα νερά πριν 25 χρόνια με την έκδοση του βιβλίου The Mathematics of Plato's Academy.]

Μία άλλη ιδιότητα των πλευρικών και διαμετρικών αριθμών είναι η ομοιότητα των 'ανθυφαιρετικών' αναπτυγμάτων τους: προσπαθώντας να βρούμε τον μέγιστο κοινό διαιρέτη τους με τον γνωστό 'Ευκλείδειο' αλγόριθμο, και αρχίζοντας με διαίρεση του δια του 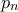, λαμβάνουμε τον ως πρώτο πηλίκο και εν συνεχεία άλλα πηλίκα ίσα προς .

'Παρόμοιο' ανθυφαιρετικό ανάπτυγμα, μη τερματιζόμενο όμως, λαμβάνουμε και όταν προσπαθήσουμε να βρούμε τον μέγιστο κοινό διαιρέτη διαμέτρου και πλευράς ισοσκελούς ορθογωνίου τριγώνου: αυτό σημαίνει, σύμφωνα με την Πρόταση 10.2 των Στοιχείων, ότι πλευρά και διάμετρος είναι 'ασύμμετρες προς άλληλες', και ότι, για παράδειγμα, ο είναι άρρητος (ανακάλυψη της ασυμμετρίας).

Πρώτος στα νεώτερα χρόνια ο G. Chrystal (1889) έδωσε γεωμετρική μορφή στην παραπάνω ανθυφαιρετική διαδικασία, δημιουργώντας μία άπειρη ακολουθία φθινόντων τετραγώνων. 130 χρόνια αργότερα, οι συγγραφείς επιχειρούν ανακατασκευή της αρχικής Πυθαγόρειας απόδειξης βασιζόμενοι σε νύξη του Πρόκλου για άπειρη ακολουθία φθινόντων γνωμόνων (εις Ευκλείδην 60, 7-12). Βεβαίως τα ανθυφαιρετικά υπόλοιπα δεν μπορούν παρά να είναι τα ίδια και στις δύο αποδείξεις, μία 'σύνθεση' των οποίων δίνεται στο συνημμένο: εικονίζονται οι δύο πρώτοι γνώμονες, 'πάχους' και , αντίστοιχα, με τα να προκύπτουν με φυσικό και γεωμετρικά όμοιο τρόπο -- και είναι ακριβώς αυτή η (αυτο-)ομοιότητα που ευθύνεται για τον μη τερματισμό της ανθυφαιρετικής διαδικασίας!

Μία σύγχρονη/αλγεβρική ματιά στα ανθυφαιρετικά υπόλοιπα αποκαλύπτει ότι , κλπ: παρατηρούμε ότι εμφανίζονται ξανά οι πλευρικοί και διαμετρικοί αριθμοί! (Αν μάλιστα χρησιμοποιήσουμε σχέσεις όπως οι ή λαμβάνουμε ανισότητες της μορφής 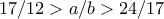, αντίστοιχα, ήδη αρκετά καλές προσεγγίσεις του .)

[Θα μπορούσαν οι πλευρικοί και διαμετρικοί αριθμοί να είχαν ανακαλυφθεί όπως στην προηγούμενη παράγραφο; Αυτό που φαίνεται προφανές σήμερα πιθανώς δεν ήταν 'αλγεβρικά εφικτό' ΤΟΤΕ, οπότε αναρωτιέται κανείς μήπως προέκυψαν 'γλαφυρώς', κατά τον αναδρομικό αλγόριθμο που 'προτείνει' άμεσα το Γλαφυρό Θεώρημα -- υπάρχει όμως και εδώ η δυσκολία ερμήνευσης της επιλογής του πρώτου βήματος, . Οι συγγραφείς θεωρούν πιθανότερο για τις ακολουθίες (και τους αντίστοιχους αναδρομικούς ορισμούς) να προέκυψαν ως πεπερασμένες προσεγγίσεις στο άπειρο ανθυφαιρετικό ανάπτυγμα διαμέτρου προς πλευρά.]

Το τελικό έξοχο σχόλιο προέρχεται από κάποιον ανώνυμο σχολιαστή του Ευκλείδη: τονίζεται ότι οι φυσικοί αριθμοί δεν 'διαιρούνται' επ' άπειρον αλλά είναι όλοι διαφορετικοί, ενώ τα αντίθετα συμβαίνουν με τα ευθύγραμμα τμήματα.

12-5-2019.pdf

(231.43 KiB) Μεταφορτώθηκε 118 φορές

[gbaloglou]

Πρώτος στα νεώτερα χρόνια ο G. Chrystal (1889) έδωσε γεωμετρική μορφή στην παραπάνω ανθυφαιρετική διαδικασία, δημιουργώντας μία άπειρη ακολουθία φθινόντων τετραγώνων. 130 χρόνια αργότερα, οι συγγραφείς επιχειρούν ανακατασκευή της αρχικής Πυθαγόρειας απόδειξης βασιζόμενοι σε νύξη του Πρόκλου για άπειρη ακολουθία φθινόντων γνωμόνων (εις Ευκλείδην 60, 7-12). Βεβαίως τα ανθυφαιρετικά υπόλοιπα δεν μπορούν παρά να είναι τα ίδια και στις δύο αποδείξεις, μία 'σύνθεση' των οποίων δίνεται στο συνημμένο: εικονίζονται οι δύο πρώτοι γνώμονες, 'πάχους' και , αντίστοιχα, με τα να προκύπτουν με φυσικό και γεωμετρικά όμοιο τρόπο -- και είναι ακριβώς αυτή η (αυτο-)ομοιότητα που ευθύνεται για τον μη τερματισμό της ανθυφαιρετικής διαδικασίας!

Παραθέτω την κατασκευή ( κλπ) του G. Chrystal από τις σελίδες 270-271 του πρώτου τόμου της Άλγεβρας του (1889/1886): αποκαλεί την συγκεκριμένη περίπτωση (ασυμμετρίας πλευράς προς διαγώνιο τετραγώνου) "historically famous", χωρίς όμως να παραθέτει οποιαδήποτε ιστορικά στοιχεία. (Γνωρίζει τον Ευκλείδη, όπου όμως η συγκεκριμένη κατασκευή δεν υπάρχει.)

GChrystal-1886.png (160.26 KiB) Προβλήθηκε 3533 φορές

[gbaloglou]

Το Γλαφυρό Θεώρημα μάς λέει ότι αν τότε , και αναλόγως , , , κοκ: ξεκινώντας από ένα ισοσκελές ορθογώνιο τρίγωνο δημιουργούμε μία ακολουθία όλο και μεγαλύτερων ισοσκελών ορθογωνίων τριγώνων (στις πλευρές των οποίων εμφανίζονται ως 'συντελεστές' οι πλευρικοί και διαμετρικοί αριθμοί).

Ένα άλλο Γλαφυρό Θεώρημα που οι συγγραφείς μάς δίνουν στην ενότητα 8.11 προκύπτει από την Πρόταση 2.9 των Στοιχείων και μας λέει ότι αν τότε , και αναλόγως , , , κοκ: ξεκινώντας και πάλι από ένα ισοσκελές ορθογώνιο τρίγωνο δημιουργούμε αυτήν την φορά μία ακολουθία όλο και μικρότερων ισοσκελών ορθογωνίων τριγώνων (στις πλευρές των οποίων εμφανίζονται και πάλι ως 'συντελεστές' οι πλευρικοί και διαμετρικοί αριθμοί).

Απλές γεωμετρικές αποδείξεις αυτού του 'αντίστροφου' γλαφυρού θεωρήματος μπορούν να δοθούν στο πνεύμα των απλών γεωμετρικών αποδείξεων του 'ευθέος'. Μία 'σύγχρονη' απόδειξη εμπεριέχεται πάντως και στην απόδειξη αρρητότητας του του Stanley Tennenbaum (που αναφέρουν οι συγγραφείς ως ουσιαστικά βασιζόμενη στην Πρόταση 2.9), όπου η ύπαρξη ενός 'ελάχιστου' ισοσκελούς ορθογωνίου τριγώνου με ακέραιες πλευρές οδηγεί άτοπα σε ακόμη μικρότερο ισοσκελές ορθογώνιο τρίγωνο με ακέραιες πλευρές:

tennenbaum.png (2.69 KiB) Προβλήθηκε 3476 φορές

[gbaloglou]

Απλές γεωμετρικές αποδείξεις αυτού του 'αντίστροφου' γλαφυρού θεωρήματος μπορούν να δοθούν στο πνεύμα των απλών γεωμετρικών αποδείξεων του 'ευθέος'.

Στο 'ευθύ' (κύριο) γλαφυρό θεώρημα ξεκινάμε από ισοσκελές ορθογώνιο τρίγωνο πλευράς και διαμέτρου και καταλήγουμε σε (μεγαλύτερο) ισοσκελές ορθογώνιο τρίγωνο πλευράς και διαμέτρου : δύο απλές γεωμετρικές κατασκευές δόθηκαν στο συνημμένο της αρχικής δημοσίευσης. (Ας παρατηρηθεί εδώ ότι ουσιαστικά/αρχικά δεν χρειάζεται καν το Πυθαγόρειο Θεώρημα, το οποίο επικαλούμαστε μόνο στο αλγεβρικό/τελικό βήμα .)

Στο 'αντίστροφο' γλαφυρό θεώρημα ξεκινάμε από ισοσκελές ορθογώνιο τρίγωνο πλευράς και διαμέτρου και καταλήγουμε σε (μικρότερο) ισοσκελές ορθογώνιο τρίγωνο πλευράς και διαμέτρου . Οι απαιτούμενες γεωμετρικές κατασκευές, αντίστοιχες αυτών που χρειάστηκαν για το 'ευθύ' γλαφυρό θεώρημα και παρουσίασα στο συνημμένο της αρχικής δημοσίευσης, είναι δυσκολότερες: στην πρώτη περίπτωση απαιτείται, νομίζω (βλ. συνημμένο), η κατασκευή ισοσκελούς τραπεζίου με τρεις πλευρές ίσες (δυνατή με κανόνα και διαβήτη αλλά όχι κατά προφανή σε μένα τρόπο, ιδίως αν δεν θέλουμε να χρησιμοποιήσουμε το Πυθαγόρειο Θεώρημα), στην δεύτερη περίπτωση η κορυφή του νέου ισοσκελούς ορθογωνίου τριγώνου είναι το έγκεντρο του αρχικού τριγώνου (βλ. συνημμένο) και τα υπόλοιπα έπονται (με την επιφύλαξη ότι η έννοια του έγκεντρου ίσως και να μην ήταν γνωστή στους Πυθαγόρειους).

αντιγλαφυρόν.png (4.42 KiB) Προβλήθηκε 3425 φορές

[gbaloglou]

Συνδυάζοντας την ιδέα του Stanley Tennenbaum της προ-προηγούμενης δημοσίευσης με το 'αντιγλαφυρό θεώρημα' της προηγούμενης δημοσίευσης ... λαμβάνουμε μία στοιχειώδη απόδειξη της ασυμμετρίας πλευράς-διαμέτρου ... που δεν χρησιμοποιεί καν το Πυθαγόρειο Θεώρημα: υποθέτοντας ότι υπάρχει κάποιο ελάχιστο ισοσκελές ορθογώνιο τρίγωνο διαμέτρου και πλευράς , δημιουργούμε νέο ισοσκελές ορθογώνιο τρίγωνο με κορυφή το έγκεντρο του αρχικού, διάμετρο , και πλευρά (άτοπο).

Το Πυθαγόρειο Θεώρημα δεν χρησιμοποιήθηκε καθώς δεν απαιτείται η συνεπαγωγή του 'αριθμητικού' γλαφυρού θεωρήματος αλλά η αμιγώς γεωμετρική 'Πρόκλεια' συνεπαγωγή "αν υπάρχει ισοσκελές ορθογώνιο τρίγωνο με διάμετρο και πλευρά τότε υπάρχει ισοσκελές ορθογώνιο τρίγωνο με διάμετρο και πλευρά ". Βεβαίως στην κατασκευή/απόδειξη του Tennenbaum το Πυθαγόρειο Θεώρημα παίζει κύριο ρόλο, καθώς χρησιμοποιείται η συνεπαγωγή .

[Μια προσεκτικότερη ματιά στις 'ανθυφαιρετικές' αποδείξεις της ασυμμετρίας πλευράς-διαμέτρου που περιλαμβάνονται στο βιβλίο των Νεγρεπόντη-Φαρμάκη δείχνει ότι ούτε αυτές απαιτούν το Πυθαγόρειο Θεώρημα: πράγματι, αρκεί να παρατηρηθεί ότι αντί της αρκεί να χρησιμοποιηθεί -- βάσει απλών γεωμετρικών συλλογισμών -- η (πρώτο βήμα), αντί της 'γνωμονικής' η (δεύτερο βήμα), κοκ]

[gbaloglou]

Ιδίας κοπής αλλά αρκετά απλούστερη η απόδειξη που έδωσε ο Άγγελος Τσιριμώκος (Putnam Fellow 1973) σε άλλη συζήτηση:

αγγελική-αρρητότητα.jpg (11.4 KiB) Προβλήθηκε 3336 φορές

[gbaloglou]

[Μια προσεκτικότερη ματιά στις 'ανθυφαιρετικές' αποδείξεις της ασυμμετρίας πλευράς-διαμέτρου που περιλαμβάνονται στο βιβλίο των Νεγρεπόντη-Φαρμάκη δείχνει ότι ούτε αυτές απαιτούν το Πυθαγόρειο Θεώρημα: πράγματι, αρκεί να παρατηρηθεί ότι αντί της αρκεί να χρησιμοποιηθεί -- βάσει απλών γεωμετρικών συλλογισμών -- η (πρώτο βήμα), αντί της 'γνωμονικής' η (δεύτερο βήμα), κοκ]

Ακριβέστερα, το Πυθαγόρειο Θεώρημα στην προτεινόμενη ανακατασκευή των Νεγρεπόντη-Φαρμάκη μπορεί να παραληφθεί μόνον αν αυτή 'ταυτισθεί' με την παραπάνω προσέγγιση του G. Chrystal ... όπως, αρκετά αυθαίρετα, έκανα στην παρουσίαση μου της 12-5-2019 (βλ. συνημμένο αρχικής δημοσίευσης), βασιζόμενος στην υποχρεωτική ταύτιση του πρώτου ανθυφαιρετικού υπολοίπου . Όμως, όπως δείχνει και το παρόν συνημμένο, πρόκειται για δύο διαφορετικούς δρόμους: σ' αυτόν του G. Chrystal (και πιθανώς προγενέστερων αυτού που αγνοούμε, και σίγουρα μεταγενέστερων αυτού που αναφέρουν οι συγγραφείς) μία απλή (;) γεωμετρική ιδέα (κάθετος στην υποτείνουσα στο σημείο όπου 'φτάνει' η πλευρά) δημιουργεί το κρίσιμο μήκος τρεις φορές (και τα υπόλοιπα έπονται), σ' αυτόν των Νεγρεπόντη-Φαρμάκη το προκύπτει, μέσω Πυθαγορείου Θεωρήματος, ως (γνωστή ήδη) 'λύση' μιας 'εξίσωσης', μιας "παραβολής χωρίων καθ' υπερβολή"*.

Η πιθανότητα να είχαν φτάσει οι Πυθαγόρειοι στην ασυμμετρία πλευράς-υποτείνουσας ισοσκελούς ορθογωνίου τριγώνου ΠΡΙΝ φτάσουν στο Πυθαγόρειο Θεώρημα είναι βέβαια σκανδαλωδώς γοητευτική (και ενισχύεται κάπως, ειρήσθω εν παρόδω, από την πιθανή μη εύρεση της 'σύγχρονης' αριθμοθεωρητικής απόδειξης από τους Πυθαγόρειους), σημαντικότερο όμως εδώ είναι το ερώτημα: γιατί να επιμένουμε σε εκ μέρους τους χρήση της ανθυφαιρετικής διαδικασίας την στιγμή που έχουμε διαθέσιμη την παραπάνω 'αντιγλαφυρή' προσέγγιση των Πρόκλου-Tennenbaum-Τσιριμώκου; Ένα επιχείρημα είναι η 'ξεκρέμαστη' Πρόταση 10.2 των Στοιχείων, ένα γενικό κριτήριο ασυμμετρίας βασισμένο σε μη περατούμενη ανθυφαίρεση, που εφαρμόζεται άμεσα στις ανθυφαιρετικές προσεγγίσεις των G. Chrystal και Νεγρεπόντη-Φαρμάκη. Ένα άλλο επιχείρημα είναι η αναφορά του Πρόκλου (Εις Ευκλείδην 60, 7-12) σε άπειρη φθίνουσα ακολουθία γνωμόνων σε σχέση με την ασυμμετρία πλευράς-υποτείνουσας ισοσκελούς ορθογωνίου τριγώνου ΚΑΙ την εκ μέρους του 'σύγκριση' γεωμετρικής και αριθμητικής ανθυφαίρεσης (βλ. συνημμένο αρχικής δημοσίευσης).

Στο πρώτο επιχείρημα θα μπορούσε να αντιτείνει κάποιος ότι η Πρόταση 10.2 χρησιμοποιήθηκε, όχι κατ' ανάγκην από τους Πυθαγόρειους, για την απόδειξη της ασυμμετρίας πλευράς-διαγωνίου κανονικού πενταγώνου (άμεσα σχετιζόμενης με την αρρητότητα της χρυσής τομής), όπως άλλωστε προτείνεται από τους συγγραφείς στην ενότητα 7.8: η ασυμμετρία αυτή ήταν επίσης γνωστή ("άλογος γαρ έστιν η τοιαύτη ευθεία και αριθμοίς ουχ υποπίπτει", Νεγρεπόντης-Φαρμάκη σελ. 351), ενώ η 'αντιγλαφυρή' προσέγγιση των Πρόκλου-Tennenbaum-Τσιριμώκου ΔΕΝ εφαρμόζεται ... καθώς οδηγεί, ξεκινώντας από κανονικό πεντάγωνο ακέραιης πλευράς και ακέραιης διαγωνίου , σε μικρότερο κανονικό πεντάγωνο (αυτό των διαγωνίων) ακέραιης πλευράς και ΜΗ ακέραιης διαγωνίου !

Στο δεύτερο επιχείρημα θα μπορούσε να αντιτείνει κάποιος ότι άπειρη φθίνουσα ακολουθία γνωμόνων υπάρχει ΚΑΙ στην προσέγγιση των Πρόκλου-Tennenbaum-Τσιριμώκου, καθώς δημιουργούνται εκεί χωρία (διαφορές ισοσκελούς ορθογώνιου τριγώνου μείον το 'επόμενο', εντός αυτού, ισοσκελές ορθογώνιο τρίγωνο) που μοιάζουν με 'κολοβούς' γνώμονες! (Βεβαίως ... για την 'αντιγλαφυρή', δια της εις άτοπον απαγωγής, απόδειξη της ασυμμετρίας πλευράς-υποτείνουσας χρειάζεται ΕΝΑ και μόνον βήμα δημιουργίας ισοσκελούς ορθογωνίου τριγώνου μικρότερου του αρχικού, θα ήταν όμως φανερό ότι η διαδικασία μπορεί να συνεχίσει επ' άπειρον.)

Προτείνεται λοιπόν ως πιθανό εναλλακτικό σενάριο η χρήση της ανθυφαίρεσης από τους Πυθαγόρειους για την απόδειξη ΜΟΝΟΝ της ασυμμετρίας πλευράς-διαγωνίου κανονικού πενταγώνου. [Βέβαια στο σενάριο αυτό υπάρχει ακόμη χώρος για ανθυφαιρετική (ανα)κατασκευή, ιδίως αυτήν του G. Chrystal, όχι τόσο απλή όσο η αντιγλαφυρή απόδειξη, αλλά πιθανώς συνυπάρχουσα με αυτήν: θα μπορούσε μάλιστα να είχε πρώτα αποδειχθεί αντιγλαφυρώς η ασυμμετρία πλευράς-υποτείνουσας, ακολούθως να είχε αποδειχθεί ανθυφαιρετικώς η ασυμμετρία πλευράς-διαγωνίου κανονικού πενταγώνου, και τελικώς να είχε αποδειχθεί και ανθυφαιρετικώς η ασυμμετρία πλευράς-υποτείνουσας. (Βλέπε και σχετική άποψη von Fritz, υποσημείωση 190, σελίδα 349 ... υπέρ της ανθυφαιρετικής απόδειξης ασυμμετρίας πλευράς-διαγωνίου κανονικού πενταγώνου ΠΡΙΝ από την ανθυφαιρετική απόδειξη ασυμμετρίας πλευράς-υποτείνουσας.)]

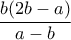*"παραβολή χωρίων καθ΄υπερβολή" είναι 'γεωμετρική εξίσωση' της μορφής , ενώ "παραβολή χωρίων κατ' έλλειψη" είναι 'γεωμετρική εξίσωση' της μορφής -- αμφότερες εξετάζονται λεπτομερώς στο Κεφάλαιο 6.

ΕΠΕΞΕΡΓΑΣΙΑ 24-5-2019 4:50 μμ: έγιναν αλλαγές στην τελευταία παράγραφο

ανθυφαιρετικώς-ή-μη.png (10.5 KiB) Προβλήθηκε 3310 φορές

[gbaloglou]

[Θα μπορούσαν οι πλευρικοί και διαμετρικοί αριθμοί να είχαν ανακαλυφθεί όπως στην προηγούμενη παράγραφο; Αυτό που φαίνεται προφανές σήμερα πιθανώς δεν ήταν 'αλγεβρικά εφικτό' ΤΟΤΕ, οπότε αναρωτιέται κανείς μήπως προέκυψαν 'γλαφυρώς', κατά τον αναδρομικό αλγόριθμο που 'προτείνει' άμεσα το Γλαφυρό Θεώρημα -- υπάρχει όμως και εδώ η δυσκολία ερμήνευσης της επιλογής του πρώτου βήματος, . Οι συγγραφείς θεωρούν πιθανότερο για τις ακολουθίες (και τους αντίστοιχους αναδρομικούς ορισμούς) να προέκυψαν ως πεπερασμένες προσεγγίσεις στο άπειρο ανθυφαιρετικό ανάπτυγμα διαμέτρου προς πλευρά.]

Μάλλον δεν θα μάθουμε ποτέ με απόλυτη βεβαιότητα πως και γιατί ανακαλύφθηκαν οι πλευρικοί και διαμετρικοί αριθμοί! Σε πολύ πρόσφατο άρθρο μας ("Από την Ρητή Διάμετρο του Πλάτωνα στο Γλαφυρό Θεώρημα του Πρόκλου", Αγγλιστί) με τον Γιάννη Θωμαΐδη (συνεισηγητή στην βιβλιοπαρουσίαση της 12-5-2019) συζητάμε διεξοδικά την μαρτυρία του Πρόκλου -- ένα σχετικά σύντομο σχόλιο επί της "Πολιτείας" -- και προτείνουμε ότι το Γλαφυρό Θεώρημα ήταν ένα 'γεωμετρικό κάλυμμα' για το γενικό επαγωγικό βήμα που μας οδηγεί από το ζεύγος στο ζεύγος ! (Στην αλγεβρική -- ή μάλλον αριθμητική -- αυτή προσέγγιση είναι και ευκολότερα ερμηνεύσιμο το πρώτο βήμα, .)

Η άποψη μας στηρίζεται κατά μεγάλο μέρος στην νέα ερμηνεία της πρότασης "Και τούτο δείκνυται δια των εν τω δευτέρω στοιχείων γραμμικώς απ' εκείνου": αφού παρατηρήσουμε ότι το "απ' εκείνου" δεν αναφέρεται σε πρόσωπο (και μάλιστα στον ίδιον τον Ευκλείδη, όπως είχε προτείνει ο Heath και είχε γίνει σιωπηρά αποδεκτό ως τώρα) αλλά σε θεώρημα που έχει ήδη αναφερθεί στο κείμενο, οπότε αναγκαστικά "εκείνο" = Γλαφυρό Θεώρημα και "τούτο" = ιδιότητα ρητών διαμέτρων (ύπαρξη άπειρης ακολουθίας ζευγών ικανοποιούντων την , "Ιδιότητα Pell"), παρατηρούμε επίσης ότι το "γραμμικώς" δεν σημαίνει υποχρεωτικά "γεωμετρικώς" αλλά μάλλον "αυστηρώς" (ότι και αν σήμαινε τότε το τελευταίο!) και καταλήγουμε στο συμπέρασμα ότι μέσα από μια φαινομενικά γεωμετρική απόδειξη (βασισμένη στην Δέκατη Πρόταση του Δευτέρου Βιβλίου των Στοιχείων) του φαινομενικά γεωμετρικού Γλαφυρού Θεωρήματος ... αποδεικνύεται αριθμητικά αυτό που οι Νεγρεπόντης & Φαρμάκη αποκαλούν Αριθμητικό Γλαφυρό Θεώρημα -- λέμε δηλαδή ότι εκεί που ο Πρόκλος γράφει "η διάμετρος γίνεται πλευρά και η πλευρά γίνεται διάμετρος" (μέσω των , , αντίστοιχα) δεν εννοεί πλέον την απλή γεωμετρική κατασκευή της παραπάνω δημοσίευσης #4 αλλά τον αλγόριθμο (που οδηγεί από την στην ) ... διευκολυνόμενος τα μέγιστα από την (Πλατωνική και Πυθαγόρεια) χρήση των όρων "ρητή πλευρά" και "ρητή διάμετρος" για τα , !

Προτείνουμε περαιτέρω ότι πιθανώς κίνητρο για τα παραπάνω δεν ήταν η δημιουργία όλο και καλύτερων προσεγγίσεων της τετραγωνικής ρίζας του (του "πλευρικού και διαμετρικού λόγου"), αλλά η 'προσέγγιση' της αδύνατης για ακεραίους από την , ή μάλλον από την 'ενθαρρυντική' -- "διο και οι Πυθαγόρειοι εθάρρησαν τη μεθόδω" -- (άμεσης συνέπειας των και ), όπως ας πούμε η ) ("οίον η εννέα μετά του μθ’ της του κε’ και δ’").

Παραθέτω το σχετικό κείμενο του Πρόκλου εδώ.

[gbaloglou]

Παραθέτω το σχετικό κείμενο του Πρόκλου εδώ.

Προσπάθησα να περικόψω το παραπάνω εδάφιο αλλά μυστηριωδώς απέτυχα: αυτό που μας ενδιαφέρει εδώ -- ειδικότερα σε σχέση με το πρόσφατο άρθρο που ανέφερα στην προηγούμενη δημοσίευση -- σταματά στο "και αεί ούτως" του Πρόκλου. Τέλος πάντων, δίνω παρακάτω σε (φρικαλέα) μονοτονική γραφή ολόκληρη την ενότητα 23 των Σχολίων του Πρόκλου στην "Πολιτεία" του Πλάτωνα, με μετάφραση και σχόλια, ελπίζοντας να συνεχίσω κάποια άλλη μέρα και με την ενότητα 27 (ή μάλλον με τμήματα της, ειδικά όσα δεν καλύπτονται εδώ).

Ότι αι ταις αρρήτοις διαμέτροις παρακείμεναι ρηταί μονάδι μείζους εισίν ή ελάττους διπλασίου, δια των αριθμών οι Πυθαγόρειοι δεικνύουσιν.

Ότι οι παρακείμενες των αρρήτων διαμέτρων [τετραγωνισμένες] ρητές διάμετροι [τετραγωνισμένες] είναι κατά μία μονάδα μεγαλύτερες ή μικρότερες του διπλασίου [των ρητών πλευρών τετραγωνισμένων], οι Πυθαγόρειοι δια των αριθμών καταδεικνύουν.

[Ας αρχίσουμε με το τελευταίο ρήμα: έχουμε λόγους να πιστεύουμε ότι, στην εποχή του Πρόκλου τουλάχιστον, το "δείκνυμι" δεν σήμαινε υποχρεωτικά και πάντοτε "αποδεικνύω", αλλά μπορούσε να σημαίνει και "επιδεικνύω": δεν ήταν δηλαδή συνδεδεμένο υποχρεωτικά με απόδειξη, αλλά ενδεχομένως μόνον με παράδειγμα! Την ασάφεια αυτή στην μεν Αγγλική αποδίδουμε με το "demonstrate", στην δε Ελληνική με το "καταδεικνύω". (Επί της ουσίας, δεν γνωρίζουμε αν οι Πυθαγόρειοι είχαν όντως δώσει απόδειξη της παραπάνω αναφερόμενης "ιδιότητας ρητών διαμέτρων" (Θωμαΐδης - Μπαλόγλου) ή "ιδιότητας Pell" (Νεγρεπόντης - Φαρμάκη) ... ή αν είχαν απλώς δώσει κάποια αριθμητικά παραδείγματα (όπως αυτά που παραθέτει ο Πρόκλος παρακάτω αλλά καιι οι προγενέστεροι Θέων και Ιάμβλιχος).)

Η ιδιιότητα Pell ή ιδιότητα ρητών διαμέτρων λέει λοιπόν ότι το τετράγωνο εκείνης της ρητής διαμέτρου που είναι κοντά ("παρακείμενη") στην άρρητη διάμετρο ή υπερβαίνει κατά μία μονάδα το διπλάσιο του τετραγώνου της αρρήτου διαμέτρου ή υπολείπεται αυτού κατά μία μονάδα. Διάμετρος είναι βεβαίως η διαγώνιος του τετραγώνου (πλευράς ) ή η υποτείνουσα του ισοσκελούς ορθογωνίου τριγώνου (πλευράς ). Από το Πυθαγόρειο Θεώρημα έχουμε , το πρόβλημα είναι ότι αυτή η σχέση δεν μπορεί να ισχύει όταν αμφότεροι οι , είναι ακέραιοι. Ισχύει όμως σε κάποιες περιπτώσεις παρά μία μονάδα, πχ ή : στις δύο αυτές περιπτώσεις οι 'μυστηριώδεις' άρρητες (δηλαδή "ανείπωτες") διάμετροι είναι αντίστοιχα οι και , και πράγματι ισχύουν οι και για τα τετράγωνα των αντίστοιχων 'παρακείμενων' ρητών διαμέτρων και (που αντιστοιχούν στις ρητές (ακέραιες) πλευρές και ).]

Επεί γαρ η μονάς πάντα εστίν σπερματικώς, δήλον, φασίν, ότι και πλευρά έστιν και διάμετρος.

Επειδή λοιπόν η μονάδα είναι από την γέννηση της τα πάντα, είναι φανερό, λέμε, ότι και πλευρά είναι και διάμετρος.

[Κανένα πρόβλημα αν έχουμε συνηθίσει στην αριθμητική χρήση των γεωμετρικών όρων "πλευρά" και "διάμετρος", καθώς ισχύει προφανώς η : ο είναι η ρητή διάμετρος παρακείμενη της αρρήτου διαμέτρου που αντιστοιχεί στην ρητή πλευρά , τόσο απλό ]

Έστων ουν δύο μονάδες, η μεν ως πλευρά η δε ως διάμετρος, και προσκείσθω τη μεν ως πλευρά μία διάμετρος, τη δε ως διαμέτρω πλευραί δύο, επείπερ η ως διάμετρος μονάδι ελάσσων ή διπλασία της ως πλευράς.

Ας είναι λοιπόν δύο μονάδες, η μία [θεωρούμενη] ως πλευρά και η άλλη ως διάμετρος, και ας παραθέσουμε [προσθέσουμε] στην μεν πλευρά μία διάμετρο, στην δε διάμετρο δύο πλευρές, με δεδομένο ότι η [θεωρούμενη] ως διάμετρος [τετραγωνισμένη] είναι διπλάσια της [θεωρούμενης] ως πλευράς [τετραγωνισμένης] παρά μία μονάδα.

[Είναι η ισότητα που αναφέρθηκε αμέσως παραπάνω ΚΑΙ η πρώτη νύξη για το Γλαφυρό Θεώρημα (που αναφέρεται 'ονομαστικά' μόνον στην ενότητα 27 του Πρόκλου) και τον αλγόριθμο του: από το ζεύγος πηγαίνουμε στο ζεύγος .]

'Εσται ουν ούτως η μεν δυείν μονάδων, η δε τριών^ και τα μεν από τούτων της μεν τεσσάρων, της δε εννέα, όπερ εστίν μονάδι μείζον ή διπλάσιον.

Οπότε η μεν [πλευρά] γίνεται δύο μονάδες, η δε [διάμετρος] τρεις^ και [τα τετράγωνα αυτών] της μεν μιας είναι τέσσερις μονάδες, της δε άλλης εννέα, δηλαδή κατά μία μονάδα μεγαλύτερο [το τετράγωνο της δεύτερης] του διπλασίου [του τετραγώνου της πρώτης].

[Από τον αλγόριθμο που αναφέραμε παραπάνω προκύπτουν οι και , οπότε : η πρώτη νύξη για το πως η οδηγεί στην .]

Πάλιν προσκείσθω τη μεν δυείν μία διάμετρος η τριών, τη δε τριών διαμέτρω δις η πλευρά ταιν δυείν.

Και πάλι ας παραθέσουμε [προσθέσουμε] στην μεν [πλευρά] των δύο [μονάδων] την διάμετρο των τριών [μονάδων], στην δε διάμετρο των τριών [μονάδων] δύο φορές την πλευρά των δύο [μονάδων].

[Το δεύτερο βήμα του αλγόριθμου: ο γίνεται (νέα πλευρά) και ο γίνεται (νέα διάμετρος).]

Έσται ουν η μεν πλευρά πέντε τινών,η δε διάμετρος επτά τινων, και τα απ' αυτών της μεν κε', της δε μθ', μονάδι ελάσσονα ή διπλάσιον.

Και η μεν πλευρά γίνεται πέντε μονάδες, η δε διάμετρος επτά μονάδες, και [τα τετράγωνα τους] της μιας 25 και της άλλης 49, κατά μία μονάδα μικρότερο [το δεύτερο] του διπλασίου [του πρώτου].

[: η οδηγεί στην .]

Ή και ο Πλάτων είπεν τον οκτώ και τετταράκοντα αριθμόν είναι από διαμέτρων ρητών μεν πεμπάδος δεομένων ενός, αρρήτων δε δεομένων δυείν, επειδή διπλάσιον η διάμετρος δύναται της πλευράς.

Γι αυτό και ο Πλάτων είπε για τον αριθμό σαράντα οκτώ ότι υπολείπεται [του τετραγώνου] της μεν ρητής διαμέτρου του πέντε κατά ένα της δε αρρήτου [διαμέτρου του πέντε] κατά δύο, επειδή η δύναμη [τετράγωνο] της [αρρήτου] διαμέτρου είναι διπλάσια της δύναμης [τετραγώνου] της πλευράς.

[Μ' αυτήν ακριβώς την πρόταση αρχίζουμε ουσιαστικά το άρθρο μας: τεράστιας σημασίας για την Ιστορία των Μαθηματικών η ισότητα που κράτησε ζωντανή την μνήμη της "ρητής διαμέτρου" (που όφειλαν να εξηγήσουν στους αναγνώστες του Πλάτωνα οι σχολιαστές του αρκετούς αιώνες αργότερα)!]

Εάν δε λάβωμεν απάσας τας από των τοιούτων διαμέτρων, έσονται διπλάσιαι όντως, ων εκάστη μονάδι μείζων ή ελάσσων διπλασίου^ οίον η εννέα μετά του μθ' της του κε' και δ'.

Εαν δε προσθέσουμε τα [τετράγωνα] όλων αυτών των διαμέτρων, προκύπτουν όντως διπλάσιες [των τετραγώνων των πλευρών], καθώς η κάθε μία [τετραγωνισμένη] είναι κατά μία μονάδα μεγαλύτερη ή μικρότερη του διπλασίου [του τετραγώνου της πλευράς]^ όπως ο εννέα μαζί με τον [είναι διπλάσιος] του 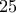συν .

[Όχι όλες τις προκύπτουσες ισότητες, αλλά δύο από αυτές προσθέτουμε κατά μέλη ώστε να λάβουμε το πολυπόθητο υποκατάστατο της αδύνατης στους ακεραίους : από πρόσθεση κατά μέλη των και προκύπτει η , πχ από τις και προκύπτει η , από τις και προκύπτει η που ΕΥΤΥΧΩΣ αναφέρει ο Πρόκλος, κοκ]

Διο και οι Πυθαγόρειοι εθάρρησαν τη μεθόδω.

Γι' αυτό και ενθαρρύνθηκαν από την μέθοδο αυτή οι Πυθαγόρειοι.

[Όπως ανέφερα και παραπάνω -- αλλά και στην προηγούμενη δημοσίευση -- το τέλος αυτό της ενότητας 23 είναι μεγάλης σημασίας (που έχει σε μεγάλο βαθμό διαφύγει της προσοχής των ερευνητών που προηγήθηκαν των Νεγρεπόντη-Φαρμάκη και ημών): φαίνεται πως οι Πυθαγόρειοι γοητεύτηκαν -- ή έστω παρηγορήθηκαν -- από τις παραπάνω προκύπτουσες και και άλλες ειδικές περιπτώσεις της αριθμητικής εκδοχής της Ευκλείδειας ΙΙ.10 () που ανακάλυψαν (αν όχι την Ευκλείδεια ΙΙ.10 στην πλήρη της γενικότητα) ... τόσο πολύ που ΙΣΩΣ να ήταν πιο σημαντική γι αυτούς από την που ΦΑΙΝΕΤΑΙ να ήταν ο κύριος στόχος τους!]

[gbaloglou]

Παραθέτω το σχετικό κείμενο του Πρόκλου εδώ.

Προσπάθησα να περικόψω το παραπάνω εδάφιο αλλά μυστηριωδώς απέτυχα: αυτό που μας ενδιαφέρει εδώ -- ειδικότερα σε σχέση με το πρόσφατο άρθρο που ανέφερα στην προηγούμενη δημοσίευση -- σταματά στο "και αεί ούτως" του Πρόκλου. Τέλος πάντων, δίνω παρακάτω σε (φρικαλέα) μονοτονική γραφή ολόκληρη την ενότητα 23 των Σχολίων του Πρόκλου στην "Πολιτεία" του Πλάτωνα, με μετάφραση και σχόλια, ελπίζοντας να συνεχίσω κάποια άλλη μέρα και με την ενότητα 27 (ή μάλλον με τμήματα της, ειδικά όσα δεν καλύπτονται εδώ).

Συνεχίζω λοιπόν με το αρχικό τμήμα της ενότητας 27 (γραμμές 1-18), ενθαρρύνοντας τους ενδιαφερόμενους να ανατρέξουν στα της προηγούμενης δημοσίευσης:

Ότι επειδή αδύνατον ρητήν είναι την διάμετρον της πλευράς ούσης ρητής (ου γαρ έστιν τετράγωνος αριθμός τετραγώνου διπλάσιος^ ώ και δήλον ότι ασύμμετρα έστιν μεγέθη, και ότι Επίκουρος ψευδώς ποιών μέτρον την άτομον πάντων σωμάτων και ο Ξενοκράτης την άτομον γραμμήν των γραμμών), επενόησαν ούτω λέγειν οι Πυθαγόρειοι και Πλάτων, της πλευράς ούσης ρητήν την διάμετρον ουχ απλώς, αλλ' εν οις δύναται τετραγώνοις, του διπλασίου λόγου, ον δει την διάμετρον ποιείν, ή μονάδι δέουσαν ή μονάδι πλεονάζουσαν^ πλεονάζουσαν μεν ως του Δ τον Θ, δέουσαν δε ως του ΚΕ τον ΜΘ.

Επειδή είναι αδύνατον η διάμετρος να είναι ρητή όταν η πλευρά είναι ρητή (διότι δεν υπάρχει τετράγωνος αριθμός διπλάσιος τετραγώνου, από το οποίο γίνεται φανερό ότι υπάρχουν ασύμμετρα μεγέθη, και ότι ο Επίκουρος εσφαλμένα έκανε την αδιαίρετη μονάδα μέτρο όλων των σωμάτων και ο Ξενοκράτης την αδιαίρετη γραμμή [μέτρο] όλων των γραμμών), έτσι οι Πυθαγόρειοι και ο Πλάτων επινόησαν να λένε ότι, δοθείσης πλευράς ρητής, η διάμετρος δεν θα είναι ρητή ως έχει, αλλά ως προς το τετράγωνό της, είτε υπολειπόμενη κατά μία μονάδα είτε υπερβαίνουσα κατά μία μονάδα τον διπλάσιο λόγο, που θα έπρεπε να έχει η διάμετρος [προς την πλευρά]^ υπερβαίνουσα μεν όπως το 9 το [διπλάσιο του] 4, υπολειπόμενη δε όπως το 49 του [διπλασίου του] 25.

[Ο Πρόκλος αρχίζει την ενότητα 27 με μία συντομότατη αναφορά στην ιστορία της ανακάλυψης της ασυμμετρίας (και της αδύνατης για ακεραίους ισότητας ), που θα άξιζε ίσως μεγαλύτερης προσοχής, αλλά όχι εδώ. Αυτό που έχει σημασία για εμάς είναι η σύνδεση της με την προσεγγιστική ισότητα (που ήδη συζήτησε ο Πρόκλος στην ενότητα 23) και η αντικατάσταση αριθμών από τα τετράγωνα τους ... για χάρη αυτής ακριβώς της προσέγγισης (ιδιότητα ρητών διαμέτρων): αυτά αποδίδονται στους Πυθαγόρειους και στον Πλάτωνα, όπως μάλλον και τα δύο συγκεκριμένα παραδείγματα () και (), που έχουν ήδη παρατεθεί στην ενότητα 23 (μαζί με την παραγωγή του δεύτερου από το πρώτο).]

Προετίθεσαν δε οι Πυθαγόρειοι τούτου τοιόνδε θεώρημα γλαφυρόν περί των διαμέτρων και πλευρών, ότι η μεν διάμετρος προσλαβούσα την πλευράν, ης έστιν διάμετρος, γίνεται πλευρά, η δε πλευρά εαυτή συντεθείσα και προσλαβούσα την διάμετρον την εαυτής γίνεται διάμετρος.

Και πριν από αυτό παρέθεσαν οι Πυθαγόρειοι ένα τόσο διαφωτιστικό θεώρημα περί των διαμέτρων και των πλευρών, ότι δηλαδή η μεν διάμετρος αυξανόμενη κατά την πλευρά της οποίας είναι διάμετρος γίνεται πλευρά, η δε πλευρά προστιθέμενη στον εαυτό της και αυξανόμενη κατά την διάμετρο της γίνεται διάμετρος.

[Το περίφημο Γλαφυρό Θεώρημα που για μία και μόνη φορά αποδίδω εδώ ως "διαφωτιστικό" (illuminating) και όχι "κομψό" (elegant) -- εκτενής φιλολογική επιχειρηματολογία υπέρ μιας τέτοιας 'νεοελληνικής' μάλλον απόδοσης βασισμένη στις χρήσεις του "γλαφυρόν" από τον Πρόκλο υπάρχει στο Παράρτημα Ι του άρθρου μας -- έχει ήδη ανεπίσημα αναφερθεί και χρησιμοποιηθεί από τον Πρόκλο στην ενότητα 23 (βλέπε και αμέσως προηγούμενη δημοσίευση). Πρόκειται ουσιαστικά για τον αλγόριθμο & ... 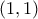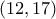που χρησιμοποιείται επίσης -- "δεικνύσθω δε επί των ρητών διαμέτρων αριθμητικώς......" -- στο τέλος της ενότητας 27, για την παραγωγή των πρώτων τεσσάρων ζευγών πλευρών-διαμέτρων και μετάβαση από το στο , από το στο , και από το στο , μια διαδικασία που ο Πρόκλος γνωρίζει ότι μπορεί να συνεχισθεί επ' άπειρον ("και αεί ούτως" γράφει αμέσως μετά τα τέσσερα παραδείγματα, κλείνοντας την ενότητα 27).]

Και τούτο δείκνυται δια των εν τω δευτέρω στοιχείων γραμμικώς απ' εκείνου.

Και αυτό αποδεικνύεται γραμμικά από εκείνο μέσω των Στοιχείων [του Ευκλείδη] του Δευτέρου [Βιβλίου].

[Η ΦΡΑΣΗ-ΚΛΕΙΔΙ: ήδη σε ανύποπτο χρόνο ο Γιάννης είχε παρατηρήσει ότι ο Πρόκλος αναφέρεται σε "γραμμική απόδειξη" του Τέταρτου Ευκλείδειου Αιτήματος (περί ισότητος όλων των ορθών γωνιών) στα Σχόλια του στον Ευκλείδη, και εμένα μου τράβηξε εξ αρχής την προσοχή εκείνο το "απ' εκείνου"! Στο Παράρτημα ΙΙ του άρθρου μας υπάρχει εκτενής επιχειρηματολογία υπέρ της απόδοσης του "γραμμικώς" ως "αυστηρώς" (αντί του καθιερωμένου "γεωμετρικώς"), και αυτό αντανακλάται στην εκ μέρους μας μη μετάφραση του (linearly): ο Πρόκλος, αλλά και ο Πάππος, χρησιμοποιούν το "γραμμικώς" ως "γεωμετρικώς" μόνον όταν αναφέρονται στο έργο του Πτολεμαίου! Όσον αφορά το "απ' εκείνου", απορρίπτουμε την συσχέτιση του (από τους προηγούμενους μελετητές, αρχίζοντας από τον Heath) με πρόσωπο (και μάλιστα ... τον ίδιον τον Ευκλείδη) υπέρ της αναφοράς του σε κάποιο κείμενο ή θεώρημα ... που, απορρίπτοντας την 'πλεοναστική' εκδοχή να είναι και πάλι το Δεύτερο (Βιβλίο των Στοιχείων), δεν μπορεί παρά να είναι το Γλαφυρό Θεώρημα (και η απόδειξη του): αυτή η επιλογή οδηγεί με την σειρά της στο συμπέρασμα ότι το "τούτο" της κρίσιμης φράσης δεν αναφέρεται στο Γλαφυρό Θεώρημα (όπως δέχονται οι προηγούμενοι μελετητές) αλλά συνδέεται με το "τούτου" της αμέσως προηγούμενης πρότασης και με όσα προηγήθηκαν της διατύπωσης του Γλαφυρού Θεωρήματος, με την αρχή της ενότητας 27 δηλαδή και με την περιγραφή της ιδιότητας των ρητών διαμέτρων!]

Ωραία τα παραπάνω, έλα όμως που ο Πρόκλος συνεχίζει με διατύπωση της Πρότασης ΙΙ.10 των Στοιχείων του Ευκλείδη -- "τα εν τω δευτέρω στοιχεία" της φράσης-κλειδί -- και χρήση αυτής προς γεωμετρική φαινομενικά απόδειξη του Γλαφυρού Θεωρήματος (πριν συνεχίσει με τα αριθμητικά παραδείγματα που ήδη ανέφερα)! Ένας τρόπος να αντιπαρέλθουμε αυτήν την δυσκολία είναι να θεωρήσουμε ότι υπάρχουν δύο παραπλήσια θεωρήματα, ένα αριθμητικό και ένα γεωμετρικό: αυτό κάνουν οι Νεγρεπόντης-Φαρμάκη, επισημαίνοντας για παράδειγμα ότι η γλώσσα (ρήματα κλπ) της γεωμετρικής απόδειξης του (γεωμετρικού) Γλαφυρού Θεωρήματος ( σε όρους αριθμητικούς) είναι παραπλήσια αυτής που χρησιμοποιείται για την παραγωγή των αριθμητικών παραδειγμάτων () στο τέλος της ενότητας 27 -- ας μην ξεχνάμε εδώ και την χρήση των γεωμετρικών όρων "πλευρά" και "διάμετρος" για αριθμούς, την ξεκάθαρη αναφορά του Πρόκλου (στα Σχόλια του στον Ευκλείδη) στην προσέγγιση της από την αλλά και στην κατ' αυτόν 'ταύτιση' Αριθμητικής και Γεωμετρίας στο Δεύτερο Βιβλίο των Στοιχείων (στα Σχόλια του στον Ευκλείδη και πάλι).

Εμείς πάμε ένα βήμα παραπέρα, βασιζόμενοι στην παραπάνω επισημανθείσα αναγγελία (στην φράση-κλειδί) του Πρόκλου όχι για απόδειξη του (γεωμετρικού) Γλαφυρού Θεωρήματος αλλά της (αριθμητικής) ιδιότητας των ρητών διαμέτρων και επίσης στην αναπάντεχη επιλογή του να χρησιμοποιήσει το "γραμμικώς" αντί του "γεωμετρικώς" (που χρησιμοποιεί σε αντιδιαστολή προς το "αριθμητικώς" στην ενότητα 35 λίγες σελίδες παρακάτω πχ), και προτείνουμε ότι δεν έχουμε να κάνουμε με δύο θεωρήματα αλλά με ένα: ο Πρόκλος δεν έχει άλλωστε άλλο κίνητρο να αποδείξει ένα γεωμετρικό θεώρημα μέσα σε μια αριθμητική ενότητα ... παρά μόνον ίσως την χρήση της οικείας στους αναγνώστες του γεωμετρικής γλώσσας για την αυστηρή απόδειξη ενός αριθμητικού θεωρήματος, ακριβέστερα μία γεωμετρική απόδειξη της από την Πρόταση ΙΙ.10 που είναι ουσιαστικά αριθμητική και διαφέρει ελάχιστα από την ξεκάθαρα και αναγκαστικά αριθμητική απόδειξη της μέσω της αριθμητικής εκδοχής της Πρότασης ΙΙ.10 ()!

Λέμε δηλαδή ότι ο Πρόκλος, πιστεύοντας ότι το κοινό του δεν είναι έτοιμο για μια αριθμητική απόδειξη της από την (αριθμητική εκδοχή της Πρότασης ΙΙ.10), παρουσιάζει μία γεωμετρικοφανή απόδειξη της παραπλήσιας (Γλαφυρό Θεώρημα) από την Πρόταση ΙΙ.10. Κάτι που στηρίζει περαιτέρω αυτήν την πιθανότητα είναι βεβαίως η ύπαρξη -- προφανής για εμάς τουλάχιστον -- απλούστερων γεωμετρικών αποδείξεων, όπως για παράδειγμα αυτές που παρατίθενται στο συνημμένο. Όπως άλλωστε εύστοχα και ... γλαφυρά συμπεραίνουν για τον ίδιο λόγο και οι Νεγρεπόντης-Φαρμάκη (σελ. 371), "η Πρόταση ΙΙ.10 δεν επινοήθηκε για ν' αποδειχθεί το γλαφυρόν θεώρημα". (Το γιατί και πως και πότε επινοήθηκε είναι μέγα θέμα που θίγουμε κάπως στο τέλος του άρθρου μας.)

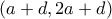Το διακύβευμα: η ύπαρξη μιας αυστηρής ("γραμμικής"), ουσιαστικά επαγωγικής (και αλγεβρικής πλέον) απόδειξης της ιδιότητας των ρητών διαμέτρων, ακριβέστερα μια απόδειξη του γενικού επαγωγικού βήματος από το στο ... και όχι απλώς η 'γεωμετρική στήριξη' συγκεκριμένων βημάτων όπως πχ από το στο -- ένα αφηρημένο (και αλγεβρικό πλέον) αποτέλεσμα (και αντίστοιχη απόδειξη) για το οποίο το κοινό του Πρόκλου ίσως δεν ήταν έτοιμο, εξ ου και η ανάγκη γεωμετρικού μανδύα ... αλλά και η χρήση του "γραμμικώς" ως μια κάποια 'προειδοποίηση' για την κατά βάθος μη γεωμετρική φύση του Γλαφυρού Θεωρήματος (και της απόδειξης του) ... και ταυτόχρονα σε αντιδιαστολή με το "αριθμητικώς" που μας εισάγει στα αριθμητικά παραδείγματα στο τέλος της ενότητας 27.

...Σταματώ εδώ, παραπέμποντας για το υπόλοιπο της ενότητας 27 (διατύπωση Πρότασης ΙΙ.10, απόδειξη Γλαφυρού Θεωρήματος, αριθμητικά παραδείγματα) στο ίδιο το άρθρο του Πρόκλου αλλά και στην ενότητα 8.6 του βιβλίου των Νεγρεπόντη-Φαρμάκη (όπου αναφέρονται και οι απόψεις προηγούμενων μελετητών σχετικά με την ύπαρξη ή μη επαγωγής στο κείμενο του Πρόκλου). Υπενθυμίζω επίσης ότι το άρθρο μας είναι διαθέσιμο εδώ (με ελάχιστα τροποποιημένη εκδοχή από 30-12-2020).

πλευροδιαμετρικώς.png (44.73 KiB) Προβλήθηκε 2174 φορές

[gbaloglou]

Συνεχίζω την ενότητα 27 με την απόδειξη του Γλαφυρού Θεωρήματος από την Πρόταση ΙΙ.10 των Στοιχείων του Ευκλείδη: όπως ήδη τόνισα στην προηγούμενη δημοσίευση, αν και όλα φαίνονται γεωμετρικά και μόνον, μάλλον κρύβουν αριθμητικές αλήθειες 'πλησίον' των γεωμετρικών, θα δούμε παρακάτω πως...

εάν ευθεία τμηθή δίχα, προσλάβη δε ευθείαν, το από της όλης συν τη προσκειμένη και το από ταύτης μόνης τετράγωνα διπλάσια τού τε από της ημισείας και του από της συγκειμένης εκ της ημισείας και της προσληφθείσης.

Αν ένα ευθύγραμμο τμήμα διχοτομηθεί και προστεθεί σ' αυτό ένα δεύτερο ευθύγραμμο τμήμα, τότε το [τετράγωνο] του αθροίσματος ολόκληρου του αρχικού τμήματος με το δεύτερο συν το [τετράγωνο] του δευτέρου μόνου του είναι διπλάσια από το [τετράγωνο] του μισού του αρχικού τμήματος συν το [τετράγωνο] του αθροίσματος του μισού του με το δεύτερο.

[Είναι η Πρόταση ΙΙ.10, γεωμετρικά διατυπωμένη, περίπου όπως στα Στοιχεία: σε σύγχρονη αλγεβρική ορολογία -- "αλγεβρική" γράφω και όχι "αριθμητική" επειδή 'προς το παρόν' ασχολούμαστε με τυχόντα ευθύγραμμα τμήματα και τα μήκη τους -- η πρόταση αυτή λέει ότι αν αρχίσουμε με τμήμα μήκους και το κόψουμε στα δύο, προσθέσουμε δε στο μισό του αρχικού τμήματος (μήκους ) ένα δεύτερο τμήμα μήκους , τότε το τετράγωνο του συν το τετράγωνο του είναι διπλάσιο του αθροίσματος του τετραγώνου του με το τετράγωνο του , δηλαδή . (Αυτό που σήμερα είναι μια εύκολη γυμνασιακή άσκηση, απλούστατο πόρισμα της γνωστής αλγεβρικής ταυτότητας για το τετράγωνο άθροισματος, ήταν τότε, και για πολλούς αιώνες μετέπειτα, κάτι μεταξύ Οδύσσειας και Γολγοθά, με την απόδειξη να παραμένει πρωτίστως γεωμετρική για αρκετούς αιώνες!)]

έστω γαρ πλευρά η ΑΒ και ίση αυτή η ΒΓ και διάμετρος της ΑΒ η ΓΔ διπλάσιον αυτής δυναμένη, δια το θεώρημα έσται το από της ΑΔ μετά του από της ΔΓ διπλάσιον του από της ΑΒ και από της ΒΔ.

Έστω λοιπόν ως πλευρά η και ίση προς αυτήν η και ως διάμετρος της η , διπλάσια σε δύναμη [τετράγωνο] της . Ένεκα του θεωρήματος [ΙΙ.10] το [τετράγωνο] της συν το [τετράγωνο] της είναι διπλάσιο του [τετραγώνου] της συν το [τετράγωνο] της .

[Θα ήταν μια απλή επαναδιατύπωση (συν τον ονοματισμό των τμημάτων) της ΙΙ.10 αν δεν εμφανίζονταν οι όροι του Γλαφυρού Θεωρήματος "πλευρά" και "διάμετρος": ο Πρόκλος θα εφαρμόσει την ΙΙ.10, στην γεωμετρική της μορφή , για να αποδείξει το Γλαφυρό Θεώρημα^ δεν είναι όμως πλέον τυχαία προσθήκη η , αφού έχει επιλεγεί να είναι διάμετρος της (πλευράς) , όπως βεβαίως επιτάσσει το Γλαφυρό Θεώρημα ("η μεν διάμετρος ...... γίνεται πλευρά, η δε πλευρά ...... γίνεται διάμετρος"). Το θέμα όμως είναι αν εδώ υπονοείται η (όπου μας σπρώχνει η γεωμετρική διατύπωση της ΙΙ.10) ή η (όπως σίγουρα επιτρέπει η χρήση των όρων "πλευρά" και "διάμετρος" στα αριθμητικά παραδείγματα που προηγήθηκαν (ενότητα 23) και που έπονται της απόδειξης του Γλαφυρού Θεωρήματος): όπως θα δούμε, η απόδειξη ισχύει και με τις δύο ερμηνείες!]

ων το από της ΔΓ διπλάσιον του από της ΑΒ^

όπου το [τετράγωνο] της είναι διπλάσιο του [τετραγώνου] της ^

[Εδώ φαίνεται να ξεκαθαρίζει το νόημα της "ως διάμετρος της η " και να λύεται το 'δίλημμα' ή υπέρ της πρώτης (γεωμετρικής) εκδοχής, ειδικά επειδή στα αριθμητικά του παραδείγματα (ενότητα 23, τέλος ενότητας 27) ο Πρόκλος τονίζει πάντοτε το "(τετράγωνο) κατά μία μονάδα μεγαλύτερο ή μικρότερο (του διπλασίου του τετραγώνου)"^ είναι όμως ο ίδιος ο Πρόκλος που στα Σχόλια του στον Ευκλείδη γράφει ότι "όταν μας αρκούν οι προσεγγίσεις, όπως στην Αριθμητική για παράδειγμα, όπου δεν έχουμε τετράγωνο αριθμού διπλάσιο άλλου τετραγώνου όπως στην Γεωμετρία, αποκαλούμε ένα τετράγωνο μικρότερο κατά ένα του διπλασίου ενός άλλου τετραγώνου διπλάσιο του"! (Βεβαίως η αριθμητική αυτή εκδοχή προϋποθέτει χρήση τμημάτων με ακέραια μήκη.) Κατά τα άλλα ... ο Πρόκλος απλώς διατυπώνει σ' αυτήν την ημιπρόταση την υπόθεση του Γλαφυρού Θεωρήματος.]

και λοιπόν άρα το από της ΑΔ του από της ΒΔ διπλάσιον^

άρα απομένει το [τετράγωνο] της να είναι διπλάσιο του [τετραγώνου] της ^

[Σ' αυτήν την ημιπρόταση ο Πρόκλος διατυπώνει το συμπέρασμα του Γλαφυρού Θεωρήματος: πράγματι από την υπόθεση ΚΑΙ την πρόταση ΙΙ.10, , έπεται η . (Περνώντας από ευθύγραμμα τμήματα σε μήκη τμημάτων, έχουμε την 'γεωμετρικο-αλγεβρική' εκδοχή του Γλαφυρού Θεωρήματος, , όπου και . Αν όμως οι , είναι ακέραιοι, ισχύει κατά τον ίδιο περίπου τρόπο, προκύπτοντας και πάλι από την (II.10), KAI η αριθμητική εκδοχή του Γλαφυρού Θεωρήματος, . Σημειώνουμε εδώ ότι οι Νεγρεπόντης-Φαρμάκη αναφέρονται σε Γεωμετρικό Γλαφυρό Θεώρημα και Αριθμητικό Γλαφυρό Θεώρημα, αντίστοιχα. Εμείς (Θωμαΐδης-Μπαλόγλου) πρεσβεύουμε ότι στο κείμενο του Πρόκλου υπάρχει ουσιαστικά μόνον το δεύτερο, καθώς το πρώτο προτείνουμε ότι είναι απλώς ένας γεωμετρικός μανδύας για το δεύτερο ... όπως άλλωστε εξέθεσα και στην αμέσως προηγούμενη δημοσίευση.)]

εάν γαρ ή ως όλον προς όλον, ούτως αφαιρεθέν προς αφαιρεθέν, έσται και το λοιπόν προς το λοιπόν ως όλον προς όλον.

Επειδή αν ένα ολόκληρο είναι προς ένα ολόκληρο όπως ένα αφαιρεθέν μέρος είναι προς ένα αφαιρεθέν μέρος, θα είναι και το υπόλοιπο προς το υπόλοιπο όπως το ολόκληρο είναι προς το ολόκληρο.

[Εδώ ο Πρόκλος επιχειρεί μία αιτιολόγηση της απόδειξης που προηγήθηκε στο πνεύμα του "αν και τότε ": ΕΑΝ επιμερίσουμε (Στοιχεία ΙΙ.1), τότε έχουμε την "αν και τότε " (απλή εφαρμογή της Κοινής Έννοιας 3 των Στοιχείων, "αν και τότε ")^ αν δεν επιμερίσουμε, τότε εχουμε επίκληση της Πρότασης V.19 των Στοιχείων (την διατύπωση της οποίας ακολουθεί το 'λήμμα' του Πρόκλου), μπερδεύονται κάπως τα πράγματα Επί της ουσίας, και σε σύγχρονους αλγεβρικούς όρους, στην μεν γεωμετρική εκδοχή του Γλαφυρού Θεωρήματος πηγαίνουμε από την ή και την στην (μέσω Πρότασης V.19 ή Κοινής Εννοίας 3, αντίστοιχα), στην δε αριθμητική εκδοχή του Γλαφυρού Θεωρήματος πηγαίνουμε από τις και στην , κλπ]

η άρα ΓΔ διάμετρος προσλαβούσα την ΒΓ πλευράν έστι πλευρά^ η δε ΑΒ εαυτήν προσλαβούσα την ΒΓ και την διάμετρον εαυτής την ΓΔ εστί διάμετρος^ δύναται γαρ διπλάσιον της πλευράς τής ΔΒ.

Οπότε η διάμετρος αυξηθείσα κατά την πλευρά γίνεται πλευρά^ η δε αυξανόμενη κατά τον εαυτό της με την και κατά την διάμετρο της γίνεται διάμετρος^ πράγματι είναι διπλάσια [ως πλέον] κατά δύναμη [τετράγωνο] της πλευράς .

[Απλώς μία συμπερασματική επαναδιατύπωση του Γλαφυρού Θεωρήματος, στην γεωμετρική του μορφή και πάλι, , δηλαδή .]

ΑΒΓΔ.png (1.02 KiB) Προβλήθηκε 2040 φορές

[gbaloglou]

Ολοκληρώνω την ενότητα 27 και την 'εκδρομή στον Πρόκλο' με τα αριθμητικά παραδείγματα για την ιδιότητα των ρητών διαμέτρων: μεγάλης σημασίας είναι η πρώτη πρόταση και η τελευταία, τα ενδιάμεσα (γνωστά σε μεγάλο βαθμό από την ενότητα 23) παρατίθενται χάριν πληρότητας.

Ταύτα μεν ουν ταύτη^ δεικνύσθω δε επί των ρητών διαμέτρων αριθμητικώς, ας είπομεν μονάδι μείζους είναι ή ελάσσους.

Και αυτά μεν όσον αφορά αυτό [το γλαφυρό θεώρημα και την απόδειξη του]^ ας δείξουμε δε σχετικά με τις ρητές διαμέτρους αριθμητικώς ότι, όπως είπαμε, είναι μεγαλύτερες ή μικρότερες κατά μία μονάδα [κατά τα τετράγωνα τους σε σχέση με το διπλάσιο τετράγωνο της αντίστοιχης πλευράς].

[Εδώ ο Πρόκλος συνδέει τα όσα προηγήθηκαν (φαινομενικά γεωμετρική απόδειξη (όσο γεωμετρική είναι τελικά η ΙΙ.10 των Στοιχείων) ενός φαινομενικά γεωμετρικού Γλαφυρού Θεωρήματος) με όσα έπονται (ξεκάθαρα αριθμητικά παραδείγματα για την ιδιότητα των ρητών διαμέτρων). Δεν παραλείπει να αντιδιαστείλει την αριθμητική φύση όσων έπονται με όσα "γραμμικά" προηγήθηκαν, χωρίς πάντως να τα έχει χαρακτηρίσει και γεωμετρικά (όπως ήδη επισημάναμε). Τονίζει επίσης ότι, από εδώ και πέρα, οι διάμετρες θα είναι ρητές -- χωρίς πάντως να ξεκαθαρίζεται πουθενά ότι σε όσα προηγήθηκαν οι διάμετροι ήταν πάντοτε άρρητες! (Ακριβέστερα, έχουμε ήδη επισημάνει/επιχειρηματολογήσει ότι οι διάμετροι και πλευρές στην διατύπωση του Γλαφυρού Θεωρήματος (και σε όσα προηγήθηκαν αυτής) είναι ρητές, παρά το γεγονός ότι οι διάμετροι και πλευρές της απόδειξης του είναι άρρητες.) Και βέβαια δεν παραλείπει ο Πρόκλος να υπενθυμίσει ότι από εδώ και πέρα θα έχουμε διαφορά μονάδος: δεν θα ισχύουν πλέον η και η συνεπαγόμενη των αρρήτων διαμέτρων, αλλά η μοιραίως 'παραπλήσια' και η ομοίως (ΙΙ.10) συνεπαγόμενη των ρητών διαμέτρων.]

έστω μονάς, περί αυτήν δε έστω μονάς, ή και πλευρά έστιν εαυτής, διότι άπαξ το εν γίνεται εν, και διάμετρος ρητή, μονάδι ποιούσα έλασσον του από της πλευράς, τούτ' έστιν του αφ' εαυτής^ αν γαρ προσλάβη μονάδα το απ' αυτής, ό έστι το έν, γίνεται του από αυτής ως πλευράς διπλάσιον.

Έστω μονάδα -- και δίπλα της άλλη μονάδα, που είναι και πλευρά του εαυτού της, διότι μία φορά το ένα γίνεται ένα -- και διάμετρος ρητή, που το τετράγωνο της είναι κατά ένα μικρότερο του [διπλασίου] τετραγώνου της πλευράς, δηλαδή του [διπλασίου] τετραγώνου του εαυτού της^ διότι αν στο τετράγωνο της, που είναι το ένα, προστεθεί η μονάδα, γίνεται διπλάσιο του τετραγώνου της [μονάδας της θεωρούμενης ως] πλευράς.

[Στην ισότητα ... η πρώτη μονάδα θεωρείται διάμετρος, και η "περί αυτήν" δεύτερη μονάδα θεωρείται πλευρά: τόσο ... απλό! (Ο είναι "πλευρά του εαυτού του" καθώς .)]

λαβέτω ουν η διαμετρική μονάς πλευράν, ό έστι μονάδα (και γαρ αύτη διάμετρος ην), γίνεται δυάς και πλευρά τετράδος^

Ας προστεθεί λοιπόν στην διαμετρική μονάδα πλευρά, που είναι μονάδα (καθώς ήταν διάμετρος και αυτή), οπότε γίνεται δυάδα και πλευρά τετράδος^

[, οπότε η διάμετρος , έχοντας αυξηθεί κατά την πλευρά , γίνεται πλευρά [2] με τετράγωνο . Ας παρατηρηθεί εδώ ότι "η διάμετρος γίνεται πλευρά", όπως ακριβώς στην διατύπωση του Γλαφυρού Θεωρήματος. Σε αντίθεση μάλιστα με την διατύπωση της ενότητας 23, όπου προστίθεται ("προσκείσθω") στην πλευρά η διάμετρος για να γίνει (και παραμείνει) πλευρά, εδώ αυξάνεται ("λαβέτω") η διάμετρος κατά την πλευρά για να γίνει πλευρά.]

η δε πλευρική μονάς εαυτή συντεθείσα λαβέτω διάμετρον άλλην μονάδα (ήν γαρ και η διαμετρική), γίνεται τριάς και ποιεί τον εννέα, μονάδι μείζονα του από δυάδος^

η δε πλευρική μονάδα προστιθέμενη στον εαυτό της ας αυξηθεί κατά την διάμετρο που είναι μία άλλη μονάδα (καθώς θεωρούνταν διάμετρος, [οπότε] γίνεται τριάδα και [τετραγωνιζόμενη] δίνει τον εννέα, κατα μία μονάδα μεγαλύτερο του [διπλασίου] τετραγώνου της δυάδας^

[, οπότε η πλευρά , έχοντας αυξηθεί κατά τον εαυτό της συν την διάμετρο , γίνεται [διάμετρος] με . Εδώ δεν αναφέρεται καν ότι η πλευρά γίνεται διάμετρος.]

και εξής η δυάς προσλαβέτω πλευρά ούσα την τριάδα διάμετρον ούσαν, γίνεται πεμπάς^

και μετά ας προστεθεί στην δυάδα, που είναι πλευρά, η τριάδα, που είναι διάμετρος, να γίνει πεντάδα^

[ (Δεν αναφέρεται καν ότι ο είναι πλευρά, ενώ επιστρέφει η 'νοοτροπία' της ενότητας 23: δεν είναι η διάμετρος () που γίνεται πλευρά (), αλλά η πλευρά () που γίνεται πλευρά ().)]

και η τριάς προσλαβούσα δις την δυάδα γίνεται επτάς.

και η τριάδα αυξανόμενη δύο φορές κατά την δυάδα γίνεται επτάδα.

[ (Δεν αναφέρονται καν οι όροι "πλευρά" και "διάμετρος", ενώ και πάλι δεν είναι η πλευρά (), αλλά η διάμετρος () που γίνεται διάμετρος (): πλήρης η απομάκρυνση από την διατύπωση του Γλαφυρού Θεωρήματος!)]

και έστι το μεν από της πεντάδος είκοσι πέντε, το δε από της επτάδος τεσσαράκοντα θ, ος έστι μονάδι ελάσσων του από της πεμπάδος.

Και το μεν τετράγωνο του είναι ο , το δε τετράγωνο του είναι ο , που είναι κατά μία μονάδα μικρότερος του [διπλασίου] τετραγώνου του .

[]

πάλιν η πεμπάς προσλαβέτω την επτάδα και η επτάς δις την πεμπάδα^

και ξανά ας αυξηθεί ο κατά τον και ο κατά δύο φορές τον ^

[Ο γίνεται και ο γίνεται . (Και πάλι η πλευρά () γίνεται πλευρά () και η διάμετρος () γίνεται διάμετρος ().)]

γίνεται ο μεν από του δώδεκα εκατόν τεσσαράκοντα τέσσαρα, ο δε από του επτακαίδεκα διακόσια ογδοήκοντα εννέα, ος έστι μονάδι μείζων ή διπλάσιος του εκατόν τεσσαράκοντα τέσσαρα^

και το μεν τετράγωνο του είναι ο , το δε τετράγωνο του είναι ο , που είναι κατά μία μονάδα μεγαλύτερος του διπλασίου του ^

[]

και αεί ούτως.

και πάντα έτσι.

[Ο Πρόκλος είναι βέβαιος ότι η ΄γλαφυρή' αυτή διαδικασία (που προκύπτει "γραμμικώς" από το Γλαφυρό Θεώρημα, ακριβέστερα από την απόδειξη του μέσω της ΙΙ.10) μπορεί να συνεχισθεί επ' άπειρον, σε σύγχρονη γλώσσα με την μορφή του αλγόριθμου , . Ένα πρώτο ερώτημα που τίθεται είναι γιατί τον ενδιαφέρει αυτή η δυνατότητα: αν σκοπός ήταν όντως η προσέγγιση της τετραγωνικής ρίζας του από ρητούς αριθμούς (κάτι που δεν προκύπτει από τις πηγές), τότε το κίνητρο είναι προφανές, καθώς τα πηλίκα όντως αποτελούν όλο και καλύτερες προσεγγίσεις του ^ αν όχι, τότε απλώς ενδιέφερε τον Πρόκλο η απειρία ζευγών ακεραίων αριθμών που μας δίνουν το καλύτερο δυνατόν αντί της αδύνατης . Το κύριο ερώτημα είναι βεβαίως από που πηγάζει αυτή η βεβαιότητα του Πρόκλου περί του αενάου της διαδικασίας: εδώ τίθεται και το μέγα θέμα αν έχουμε ή όχι να κάνουμε με μια πρώιμη μορφή επαγωγής (βλέπετε σχετικά και Νεγρεπόντη-Φαρμάκη σελ. 376-393), εμείς πρεσβεύουμε ότι η γεωμετρική απόδειξη του Γλαφυρού Θεωρήματος είναι ουσιαστικά μία απόδειξη του γενικού επαγωγικού βήματος (από σε , από την στην ... ακολουθώντας κατά βήμα την φαινομενικά γεωμετρική απόδειξη (από την ΙΙ.10) της ), εξ ου και η βεβαιότητα του Πρόκλου...]