δηλαδή πώς τυποποιούμαι (formalize) το:
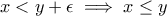

Μήπως το :
![\forall x\forall y\forall\epsilon[\epsilon>0\wedge x<y+\epsilon \implies x\leq y] \forall x\forall y\forall\epsilon[\epsilon>0\wedge x<y+\epsilon \implies x\leq y]](/forum/ext/geomar/texintegr/latexrender/pictures/3168a150e59d4a342a64a3d31b32c595.png) είναι σωστό
είναι σωστό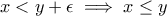

![\forall x\forall y\forall\epsilon[\epsilon>0\wedge x<y+\epsilon \implies x\leq y] \forall x\forall y\forall\epsilon[\epsilon>0\wedge x<y+\epsilon \implies x\leq y]](/forum/ext/geomar/texintegr/latexrender/pictures/3168a150e59d4a342a64a3d31b32c595.png) είναι σωστό
είναι σωστόευχαριστώ και σύμφωνα με αυτό τον τύπο πιά θα είναι η υπόθεση στην απόδειξη
 σωστό
σωστό .
.Και τώρα η απόδειξη¨
 .
.
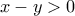
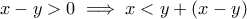 από την (1) και χρησιμοποιώντας τον κανόνα της λογικής (universal elimination) όπου
από την (1) και χρησιμοποιώντας τον κανόνα της λογικής (universal elimination) όπου 
 άτοπον
άτοπον
 χρησιμοποιώντας τον κανόνα της τριχοτόμησης των πραγματικών αριθμών
χρησιμοποιώντας τον κανόνα της τριχοτόμησης των πραγματικών αριθμών .
.
![\forall x\forall y[(\forall\epsilon(\epsilon>0\implies x<y+\epsilon))\implies x\leq y] \forall x\forall y[(\forall\epsilon(\epsilon>0\implies x<y+\epsilon))\implies x\leq y]](/forum/ext/geomar/texintegr/latexrender/pictures/cbf3ffd8bdffb61ed556a78c50663864.png)
Σωστά είναι αυτά που γράφεις, όμως δεν καταλαβαίνω γιατί χρειάζεται τόσος φορμαλισμός.labrosb έγραψε: ↑Τρί Νοέμ 30, 2021 2:48 amΚαι τώρα η απόδειξη¨
1)Υπόθεση:.
2) Υπόθεση προς άτοπον:
3)
4)από την (1) και χρησιμοποιώντας τον κανόνα της λογικής (universal elimination) όπου
5)άτοπον
6)
7)χρησιμοποιώντας τον κανόνα της τριχοτόμησης των πραγματικών αριθμών
8) Άρα:.
9) Και γενικεύοντας έχουμε:
Άρα ο τύπος που χρησιμοποιήσαμε για την τυποποίηση του θεωρήματος είναι σωστός
Σωστά;
Συγνώμη θα ήθελα να προσθέσω ότι από την 4 πάμε στην 5 χρησιμοποιώντας την 3 και 4 και τον κανόνα αποσπάσεως (modus ponens)
Συγνώμη αλλά δεν χρησιμοποίησα πλήρη φορμαλισμό αλλά όπου έπρεπε για να δούμε αν ο φορμαλισμός του παραπάνω θεωρήματος ήταν σωστόςstranger έγραψε: ↑Τρί Νοέμ 30, 2021 11:38 pmΣωστά είναι αυτά που γράφεις, όμως δεν καταλαβαίνω γιατί χρειάζεται τόσος φορμαλισμός.labrosb έγραψε: ↑Τρί Νοέμ 30, 2021 2:48 amΚαι τώρα η απόδειξη¨
1)Υπόθεση:.
2) Υπόθεση προς άτοπον:
3)
4)από την (1) και χρησιμοποιώντας τον κανόνα της λογικής (universal elimination) όπου
5)άτοπον
6)
7)χρησιμοποιώντας τον κανόνα της τριχοτόμησης των πραγματικών αριθμών
8) Άρα:.
9) Και γενικεύοντας έχουμε:
Άρα ο τύπος που χρησιμοποιήσαμε για την τυποποίηση του θεωρήματος είναι σωστός
Σωστά;
Συγνώμη θα ήθελα να προσθέσω ότι από την 4 πάμε στην 5 χρησιμοποιώντας την 3 και 4 και τον κανόνα αποσπάσεως (modus ponens)
Στα σύγχρονα μαθηματικά δεν χρησιμοποιούμε τόσο πολύ φορμαλισμό. Αυτό το κάνουμε γιατί εκτός από πολύ χρονοβόρο, δεν βοηθάει και πολύ στην κατανόηση των μαθηματικών εννοιών.
Βέβαια όλα στα μαθηματικά ξενικάνε από τα αξιώματα, όμως συνήθως χρησιμοποιούνται λέξεις αντί για σύμβολα.
Τώρα μπορεί να ρωτήσει κανείς αφού όλα εξάγονται με αυστηρό φορμαλισμό από τα αξιώματα, πως εμείς μπορούμε να κάνουμε μαθηματικά χωρίς αυτόν τον φορμαλισμό.
Η σωστή οπτική είναι ότι δεν χρησιμοποιούμε αυστηρά επιχειρήματα όμως αν χρειαστεί μπορούμε να τα μετατρέψουμε σε φορμαλισμό(που ποτέ δεν χρειάζεται).
Η συμβουλή μου είναι να μη χρησιμοποιείς αυστηρό φορμαλισμό γιατί νομίζω ότι δεν θα σε βοηθήσει να κατανοήσεις μαθηματικές έννοιες.
Χρειάζεται δηλαδή να ανοίξει κάπως το μυαλό σου(με τη καλή έννοια) και αυτό θα γίνει μελετώντας συστηματικά σύγχρονα μαθηματικά επιχειρήματα.
Αυτή είναι η γνώμη μου, χωρίς να θέλω να σε προσβάλω.
![\forall x\forall y[(\forall\epsilon(\epsilon>0\wedge x<y+\epsilon\implies x\leq y))] \forall x\forall y[(\forall\epsilon(\epsilon>0\wedge x<y+\epsilon\implies x\leq y))]](/forum/ext/geomar/texintegr/latexrender/pictures/19f7e170647df64ad81e639086b81b2b.png) επίσης οδηγεί σε σωστή λύση του προβλήματος αν ναι τότε οι δυο φόρμουλες είναι ισοδύναμες .Πως αποδεικνύουμε αυτό;
επίσης οδηγεί σε σωστή λύση του προβλήματος αν ναι τότε οι δυο φόρμουλες είναι ισοδύναμες .Πως αποδεικνύουμε αυτό;
Θα συμφωνήσω ΑΠΟΛΥΤΑ με τον stranger. Για να εξηγούμαι:
 έχουν την ιδιότητα ότι για κάθε ρητό
έχουν την ιδιότητα ότι για κάθε ρητό  με
με  ισχύει
ισχύει 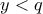 , τότε ισχύει
, τότε ισχύει  . (Απλό και άμεσο, σχεδόν τετριμμένο, χωρίς να χρειαστεί να μπούμε σε υπερβολικό φορμαλισμό).
. (Απλό και άμεσο, σχεδόν τετριμμένο, χωρίς να χρειαστεί να μπούμε σε υπερβολικό φορμαλισμό). συγκλίνουσες ακολουθίες και αν για κάθε
συγκλίνουσες ακολουθίες και αν για κάθε  ισχύει
ισχύει  , τότε
, τότε  . (Γνωστό και χιλιοειπωμένο).
. (Γνωστό και χιλιοειπωμένο).τι είναι επιχείρημα και τι πρέπει να κάνουμε για να διαπιστώσουμε εάν ένα επιχείρημα είναι σωστό η λάθος
Προσπαθώ να καταλάβω τι λες.
Όταν λέω σύγχρονο μαθηματικό επιχείρημα εννοώ μια απόδειξη που δεν κάνει επίκληση σε αξιώματα και ίσως αφήνει κάποιες(ίσως μικρές) λεπτομέρειες αναπόδεικτες και ο αναγνώστης μπορεί να τις αποδείξει μόνος του(αν θέλει) έτσι ώστε να μην χάνεται η κεντρική ιδέα της απόδειξης.
 τότε
τότε 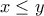 χρησιμοποιεί την δική σου απόδειξη. Τότε για να αποδείξει ένα εύκολο και εμφανές θεώρημα θα χρειαστεί τεράστιο όγκο σελιδών και προσπάθειας, ενώ η κεντρική ιδέα της απόδειξης θα έχει συσκοτιστεί ολότελα.
χρησιμοποιεί την δική σου απόδειξη. Τότε για να αποδείξει ένα εύκολο και εμφανές θεώρημα θα χρειαστεί τεράστιο όγκο σελιδών και προσπάθειας, ενώ η κεντρική ιδέα της απόδειξης θα έχει συσκοτιστεί ολότελα.Δεν πήρα απάντηση στην ερώτηση ποιο θεώρημα,αξίωμα,ορισμός,κανόνας της λογικής δικαιολογεί την ισότηταstranger έγραψε: ↑Πέμ Δεκ 02, 2021 1:18 pmΌταν λέω σύγχρονο μαθηματικό επιχείρημα εννοώ μια απόδειξη που δεν κάνει επίκληση σε αξιώματα και ίσως αφήνει κάποιες(ίσως μικρές) λεπτομέρειες αναπόδεικτες και ο αναγνώστης μπορεί να τις αποδείξει μόνος του(αν θέλει) έτσι ώστε να μην χάνεται η κεντρική ιδέα της απόδειξης.
Δηλαδή φαντάσου μια μαθηματική απόδειξη που για να δείξεις ότι "αν για κάθετότε
χρησιμοποιεί την δική σου απόδειξη. Τότε για να αποδείξει ένα εύκολο και εμφανές θεώρημα θα χρειαστεί τεράστιο όγκο σελιδών και προσπάθειας, ενώ η κεντρική ιδέα της απόδειξης θα έχει συσκοτιστεί ολότελα.
Αν απλά θες να δεις ποια είναι τα αξιώματα που χρησιμοποιούνται για να αποδειχθεί το ζητούμενο, τότε είσαι οκ.
Απλά η ένστασή μου είναι ότι αν ενδιαφέρεσαι να μάθεις μαθηματικά, τότε θα χρειαστεί κάποια πράγματα να τα αφήσεις πίσω σου(όπως για παράδειγμα τον τόσο αυστηρό φορμαλισμό).
Τέτοιος αυστηρός φορμαλισμός δεν χρησιμοποιείται ούτε στην μαθηματική λογική.

![\forall x\forall y[(\forall\epsilon(\epsilon>o\wedge x<y+\epsilon\implies x\leq y))] \forall x\forall y[(\forall\epsilon(\epsilon>o\wedge x<y+\epsilon\implies x\leq y))]](/forum/ext/geomar/texintegr/latexrender/pictures/e74cbeae8a50ea97be96179862c67511.png) οδηγεί σε σωστή απόδειξη επίσης
οδηγεί σε σωστή απόδειξη επίσηςΔεν χρειάζεται να εξάπτεσαι. Όλοι εδώ πέρα λέμε τη γνώμη μας και πως βλέπουμε τα μαθηματικά.labrosb έγραψε: ↑Πέμ Δεκ 02, 2021 9:12 pmΔεν πήρα απάντηση στην ερώτηση ποιο θεώρημα,αξίωμα,ορισμός,κανόνας της λογικής δικαιολογεί την ισότηταstranger έγραψε: ↑Πέμ Δεκ 02, 2021 1:18 pmΌταν λέω σύγχρονο μαθηματικό επιχείρημα εννοώ μια απόδειξη που δεν κάνει επίκληση σε αξιώματα και ίσως αφήνει κάποιες(ίσως μικρές) λεπτομέρειες αναπόδεικτες και ο αναγνώστης μπορεί να τις αποδείξει μόνος του(αν θέλει) έτσι ώστε να μην χάνεται η κεντρική ιδέα της απόδειξης.
Δηλαδή φαντάσου μια μαθηματική απόδειξη που για να δείξεις ότι "αν για κάθετότε
χρησιμοποιεί την δική σου απόδειξη. Τότε για να αποδείξει ένα εύκολο και εμφανές θεώρημα θα χρειαστεί τεράστιο όγκο σελιδών και προσπάθειας, ενώ η κεντρική ιδέα της απόδειξης θα έχει συσκοτιστεί ολότελα.
Αν απλά θες να δεις ποια είναι τα αξιώματα που χρησιμοποιούνται για να αποδειχθεί το ζητούμενο, τότε είσαι οκ.
Απλά η ένστασή μου είναι ότι αν ενδιαφέρεσαι να μάθεις μαθηματικά, τότε θα χρειαστεί κάποια πράγματα να τα αφήσεις πίσω σου(όπως για παράδειγμα τον τόσο αυστηρό φορμαλισμό).
Τέτοιος αυστηρός φορμαλισμός δεν χρησιμοποιείται ούτε στην μαθηματική λογική.
Πάρτε λοιπόν ένα εύκολο και εμφανές θεώρημα και κάντε μια απόδειξη σαν τη δική μου και ελάτε να μετρήσουμε τον όγκο των σελίδων
Ας πούμε το θεώρημα 0χ=0 πόσες σελίδες θα πάρει .
Ας πούμε ότι αυτό το σύγχρονο βιβλίο έχει μία απόδειξη λάθος τότε τι κάνουμε;
Επί τη ευκαιρία ο τύποςοδηγεί σε σωστή απόδειξη επίσης
Ο Angelo Margaris λοιπόν στο βιβλίο του FIRST ORDER MATHEMATICAL LOGIC Αποδεικνύει μέσα ΔΕΚΑ ΣΕΛΙΔΕΣ (127-137 26 ΘΕΩΡΗΜΑΤΑ των φυσικών αριθμών αρχίζοντας από τα αξιώματα του Πεάνο με πλήρη ΦΟΡΜΑΛΙΣΜΌ (formal proofs)
Λάθος. Σκοπός του βιβλίου αυτού είναι να δείξει πως οι κανόνες της λογικής αλληλεπιδρούν με τα αξιώματα,θεωρήματα,ορισμούς,για να παράξουν μια αλάνθαστη μαθηματική απόδειξη
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης