
Η λάθος απόδειξη μου είναι:

Ξέρουμε ότι:
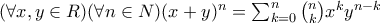
Συνεπώς:

Καί

Και

Συνεπώς

Καί

Μετά συνειδητοποίησα ότι δε γίνονται οι συγκρίσεις λόγω του:

Μπορώ να το αποδείξω και για περιττούς αλλά όχι για άρτιους n
Έχετε κάποια άλλη ιδέα;
Συντονιστής: nkatsipis


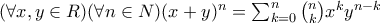







Είναι αρκετά απλό αν το δεις σωστά, γι' αυτό θα σου δώσω μόνο υπόδειξη. Μάλιστα μπορούμε να κάνουμε ουσιαστική γενίκευση δείχνοντας ότι ισχύει
 για όλους τους φυσικούς
για όλους τους φυσικούς  με
με  .
. και χρήση για το πέρασμα από το
και χρήση για το πέρασμα από το  στο
στο  της ταυτότητας
της ταυτότητας  .
.  θα χρειαστεί να το αναπτύξεις με χρήση του διωνύμου που ουσιαστικά σημαίνει ότι γράφεις το
θα χρειαστεί να το αναπτύξεις με χρήση του διωνύμου που ουσιαστικά σημαίνει ότι γράφεις το  ως γραμμικό συνδυασμό ως προς των
ως γραμμικό συνδυασμό ως προς των 
Μα αυτό είναι το εύκολο μέρος της άσκησης, και ουσιαστικά το έχω κάνει λιανά παραπάνω. Το επαναλαμβάνω:jimangel2001 έγραψε: ↑Παρ Μάιος 14, 2021 12:42 pmΕυχαριστώ πολύ για την απάντηση,
Προσπάθησα να εφαρμόσω αυτά που μου υποδείξατε και ως ειδική και ως γενική λύση όμως μάλλον κολλάω στο τελευταίο μέρος με τον γραμμικό συνδυασμό, όπου μου εμφανιζεται διπλή σούμα και δε μπορώ να τη διαχειριστώ στη προκειμένη.
 θα χρειαστεί να το αναπτύξεις με χρήση του διωνύμου"
θα χρειαστεί να το αναπτύξεις με χρήση του διωνύμου" ![\displaystyle{ (j-1+1)^{k-1} = [(j-1)+1]^{k-1} = (a+1) ^ {k-1}} \displaystyle{ (j-1+1)^{k-1} = [(j-1)+1]^{k-1} = (a+1) ^ {k-1}}](/forum/ext/geomar/texintegr/latexrender/pictures/a9558ceef3b3e01ebba903475bd538dc.png) . Συνέχισε.
. Συνέχισε. μπορεί να δειχθεί και με ισχυρά εργαλεία ανάλυσης.
μπορεί να δειχθεί και με ισχυρά εργαλεία ανάλυσης.
 τέτοιο ώστε:
τέτοιο ώστε: 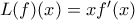 για κάθε
για κάθε  και κάθε απείρως παραγωγίσιμη συνάρτηση
και κάθε απείρως παραγωγίσιμη συνάρτηση  .
. είναι πολυώνυμο με ρίζα πολλαπλότητας
είναι πολυώνυμο με ρίζα πολλαπλότητας  το
το  , τότε το
, τότε το  είναι πολυώνυμο με ρίζα πολλαπλότητας
είναι πολυώνυμο με ρίζα πολλαπλότητας 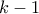 το
το  .
. me
me 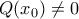 , τότε
, τότε ![\displaystyle{L(P)(x) = xP'(x) = x\left[(x - x_0)^{k}Q'(x) + k(x - x_0)^{k-1}Q(x)\right] = (x - x_0)^{k-1}\left[x(x - x_0)Q'(x) + kxQ(x)\right]} \displaystyle{L(P)(x) = xP'(x) = x\left[(x - x_0)^{k}Q'(x) + k(x - x_0)^{k-1}Q(x)\right] = (x - x_0)^{k-1}\left[x(x - x_0)Q'(x) + kxQ(x)\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/9a53b7643b5d6eaad59387d187da4bae.png) ,
,  όταν
όταν  .
. , τότε για κάθε
, τότε για κάθε  έχουμε
έχουμε
 . Για
. Για  έχουμε
έχουμε  και απλά χρησιμοποιούμε το διωνυμικό ανάπτυγμα που δίνει το δεξί μέλος της ζητούμενης για
και απλά χρησιμοποιούμε το διωνυμικό ανάπτυγμα που δίνει το δεξί μέλος της ζητούμενης για  . Έστω πως ισχύει για
. Έστω πως ισχύει για  , οπότε
, οπότε 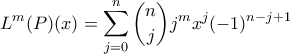 ,
, παίρνουμε:
παίρνουμε: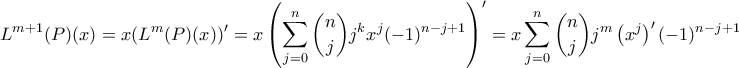 ,
,
 .
. είναι ρίζα τάξης
είναι ρίζα τάξης  (δηλαδή διπλή ρίζα) του
(δηλαδή διπλή ρίζα) του  , όπου για κάθε
, όπου για κάθε  ο 2ος ισχυρισμός δίνει:
ο 2ος ισχυρισμός δίνει: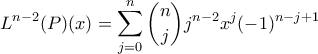 ,
, παίρνουμε:
παίρνουμε: ,
, μπορεί να είναι οποιοσδήποτε
μπορεί να είναι οποιοσδήποτε  , αφού για κάθε τέτοιο
, αφού για κάθε τέτοιο  παίρνουμε το
παίρνουμε το  που έχει ρίζα πολλαπλότητας
που έχει ρίζα πολλαπλότητας  το
το  , οπότε μηδενίζεται στο
, οπότε μηδενίζεται στο  για κάθε τέτοιο
για κάθε τέτοιο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης