 διακεκριμένοι πρώτοι όλοι
διακεκριμένοι πρώτοι όλοι  .
.Να δείξετε ότι
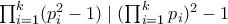 αν και μόνο αν
αν και μόνο αν 
Συντονιστής: nkatsipis
 διακεκριμένοι πρώτοι όλοι
διακεκριμένοι πρώτοι όλοι  .
.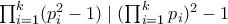 αν και μόνο αν
αν και μόνο αν 
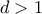 και
και  φυσικός αριθμός τότε αν
φυσικός αριθμός τότε αν  τότε ο
τότε ο  είναι πρώτος, όπου
είναι πρώτος, όπου  η ολική συνάρτηση του Euler. Είναι ανοιχτό πρόβλημα.
η ολική συνάρτηση του Euler. Είναι ανοιχτό πρόβλημα.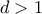 με
με  ισχύει
ισχύει  .
.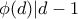 και ο
και ο  δεν είναι πρώτος:
δεν είναι πρώτος: είναι
είναι 

 έχει τουλάχιστον
έχει τουλάχιστον  πρώτους διαιρέτες
πρώτους διαιρέτεςΘα το δείξω για οποιασδήποτε μορφής διακεκριμένους πρώτους. Έστω
 το σύνολο όλων των πρώτων. Έχουμε
το σύνολο όλων των πρώτων. Έχουμε
 είναι θετικός ακέραιος, άρα
είναι θετικός ακέραιος, άρα  . Όμως για
. Όμως για  είναι απλό να δειχθεί επαγωγικά ότι
είναι απλό να δειχθεί επαγωγικά ότι  , άτοπο.
, άτοπο.Το α) είναι αρκετά απλό και το απέδειξε πρώτος ο Lehmer όταν διατύπωνε την εικασία του Lehmer.
 διαιρείται από τετράγωνο πρώτου
διαιρείται από τετράγωνο πρώτου  τότε
τότε 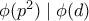 και επειδή
και επειδή  αυτό σημαίνει
αυτό σημαίνει  . Άρα ο
. Άρα ο  διαιρεί το
διαιρεί το  και το
και το  , το οποίο είναι άτοπο.
, το οποίο είναι άτοπο.Η ανισότητα
 δεν ισχύει. Ισχύει η ανάποδη. Δηλαδή ισχύει η
δεν ισχύει. Ισχύει η ανάποδη. Δηλαδή ισχύει η  για
για  και
και  .
.Έστω ότι ισχύει η δεύτερη πρόταση.
 ο ελάχιστος σύνθετος με
ο ελάχιστος σύνθετος με  .
. . Έστω
. Έστω  . Τότε έχουμε
. Τότε έχουμε  . Άρα
. Άρα  .Όμως
.Όμως  επειδή
επειδή  γιατί αλλιώς θα είχαμε
γιατί αλλιώς θα είχαμε  , το οποίο είναι άτοπο αφού ο
, το οποίο είναι άτοπο αφού ο  είναι σύνθετος.
είναι σύνθετος. και
και  , το οποίο σημαίνει ότι ο
, το οποίο σημαίνει ότι ο  είναι πρώτος.
είναι πρώτος. .
. είναι squarefree(βλεπε ποστ 6) παίρνουμε
είναι squarefree(βλεπε ποστ 6) παίρνουμε  που είναι άτοπο επειδή ο
που είναι άτοπο επειδή ο  είναι σύνθετος και ο
είναι σύνθετος και ο  είναι πρώτος και το συμπέρασμα έπεται.
είναι πρώτος και το συμπέρασμα έπεται.Ακριβώς επειδή ισχύει η ανάποδη περνώ άτοπο.
 έχουμε
έχουμε  με
με  αφού
αφού 
 άρα
άρα 


 και
και  ισχύει η ανάποδη.
ισχύει η ανάποδη.
Τελικά έχεις δίκιο και σου ζητώ συγγνώμη. Είσαι σωστός και μάλιστα με πιο σύντομη απόδειξη από εμένα. Απλά δεν είχες γράψει την απόδειξη και δεν το έβλεπα σωστό.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες