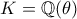 όπου
όπου  .
.Συντονιστής: nkatsipis
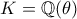 όπου
όπου  .
.Βγάζωbouzoukman έγραψε: ↑Πέμ Μαρ 26, 2020 7:12 amΝα βρεθεί μία βάση για το δακτύλιο των ακεραίων του σώματοςόπου
.
 . Μπορεί κάποιος να επιβεβαιώσει , πριν γράψω την ιδέα που έχω;
. Μπορεί κάποιος να επιβεβαιώσει , πριν γράψω την ιδέα που έχω;
Ναι αυτή είναι μία βάση!Tolaso J Kos έγραψε: ↑Πέμ Μαρ 26, 2020 11:35 amΒγάζω. Μπορεί κάποιος να επιβεβαιώσει , πριν γράψω την ιδέα που έχω;
 και ένα αλγεβρικό στοιχείο
και ένα αλγεβρικό στοιχείο  πάνω από το
πάνω από το  με ελάχιστο πολυώνυμο
με ελάχιστο πολυώνυμο  βαθμού
βαθμού  τότε μία βάση του
τότε μία βάση του  είναι η
είναι η  . Εδώ το ελάχιστο πολυώνυμο είναι
. Εδώ το ελάχιστο πολυώνυμο είναι  διότι είναι irreducible πάνω από το
διότι είναι irreducible πάνω από το  . Η βάση έπεται.
. Η βάση έπεται.
 τότε ο δακτύλιος των ακεραίων του
τότε ο δακτύλιος των ακεραίων του  έχει βάση την
έχει βάση την 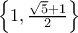 και όχι την
και όχι την 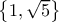 ,παρότι το ελάχιστο πολυώνυμο του
,παρότι το ελάχιστο πολυώνυμο του  υπέρ του
υπέρ του  είναι το
είναι το  .
.
 είναι μια βάση. (Αν είναι λάθος αυτό που μαντέψαμε δεν πειράζει, θα διορθωθεί αργότερα.)
είναι μια βάση. (Αν είναι λάθος αυτό που μαντέψαμε δεν πειράζει, θα διορθωθεί αργότερα.) . Αν
. Αν  οι άλλες δύο ρίζες του πολυωνύμου τότε έχουμε
οι άλλες δύο ρίζες του πολυωνύμου τότε έχουμε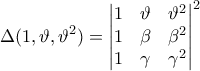

 το ελάχιστο πολυώνυμο του
το ελάχιστο πολυώνυμο του  και
και  το norm ενός στοιχείου.
το norm ενός στοιχείου. και
και 
 είναι ελεύθερος τετραγώνου, τότε η
είναι ελεύθερος τετραγώνου, τότε η  είναι βάση του δακτυλίου ακεραίων.
είναι βάση του δακτυλίου ακεραίων. ώστε ο
ώστε ο  να διαιρεί τη διακρίνουσα αν κάποιο από τα στοιχεία
να διαιρεί τη διακρίνουσα αν κάποιο από τα στοιχεία  είναι αλγεβρικός ακέραιος (όπου
είναι αλγεβρικός ακέραιος (όπου  . Αν όχι, τότε έχουμε ήδη τη βάση που θέλουμε. Αλλιώς βελτιώνουμε αυτό που μαντέψαμε για βάση και επαναλαμβάνουμε.]
. Αν όχι, τότε έχουμε ήδη τη βάση που θέλουμε. Αλλιώς βελτιώνουμε αυτό που μαντέψαμε για βάση και επαναλαμβάνουμε.]Τέλεια! Αυτή την απόδειξη είχα κι εγώ στο μυαλό μου!
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες