stranger έγραψε: ↑Τετ Μαρ 25, 2020 7:52 am
Ας βάλουμε και μία από την Πολλαπλασιαστική Θεωρία Αριθμών.
Να δείξετε ότι

καθώς

.
Το άθροισμα στο αριστερό μέλος είναι πάνω από τους πρώτους

. Η συνάρτηση

είναι το πλήθος των πρώτων διαιρετών του

.
Έστω

και

ένας πρώτος με

.
Από ευκλείδεια διαίρεση έχουμε
![\frac{n}{p} = [\frac{n}{p}] + \frac{n mod p}{p} \frac{n}{p} = [\frac{n}{p}] + \frac{n mod p}{p}](/forum/ext/geomar/texintegr/latexrender/pictures/a0cbd2d008ddc132ae2757ab493cdec3.png)
, όπου

το υπόλοιπο της ευκλείδειας διαίρεσης του

με το

.
Αθροίζοντας έχουμε
![n \sum_{p \leq n} \frac{1}{p} = \sum_{p \leq n} [\frac{n}{p}] + \sum_{p \leq n} \frac{nmodp}{p} n \sum_{p \leq n} \frac{1}{p} = \sum_{p \leq n} [\frac{n}{p}] + \sum_{p \leq n} \frac{nmodp}{p}](/forum/ext/geomar/texintegr/latexrender/pictures/113a45abe8dce59cdd25bcde8288b07b.png)
, οπότε
![\sum_{p \leq n} \frac{1}{p} = \frac{1}{n}\sum_{p \leq n} [\frac{n}{p}] + \frac{1}{n}\sum_{p \leq n} \frac{nmodp}{p} \sum_{p \leq n} \frac{1}{p} = \frac{1}{n}\sum_{p \leq n} [\frac{n}{p}] + \frac{1}{n}\sum_{p \leq n} \frac{nmodp}{p}](/forum/ext/geomar/texintegr/latexrender/pictures/0dd6bf07b9abe3994e09b626f56b1345.png)
.
Επίσης,

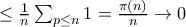
καθώς

.
Οπότε αρκεί να δείξουμε ότι
![\sum_{p \leq n} [\frac{n}{p}] = \sum_{k=1}^{n} \omega(k) \sum_{p \leq n} [\frac{n}{p}] = \sum_{k=1}^{n} \omega(k)](/forum/ext/geomar/texintegr/latexrender/pictures/bfb78f9d7c8592daf9505f1969926766.png)
(1). Θα χρησιμοποιήσουμε μαθηματική επαγωγή.
Για

έχουμε ότι η (1) ισχύει.
Έστω ότι ισχύει για

, δηλαδή
![\sum_{p \leq n} [\frac{n}{p}] = \sum_{k=1}^{n} \omega(k) \sum_{p \leq n} [\frac{n}{p}] = \sum_{k=1}^{n} \omega(k)](/forum/ext/geomar/texintegr/latexrender/pictures/bfb78f9d7c8592daf9505f1969926766.png)
.
Παίρνουμε δύο περιπτώσεις. Αν ο

είναι πρώτος τότε
![\sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] +1 \sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] +1](/forum/ext/geomar/texintegr/latexrender/pictures/60d1cc496fa3e9e2ea4fe45562ab19f6.png)
.
Επίσης, για κάθε

έχουμε
![[\frac{n+1}{p}] = [\frac{n}{p}] [\frac{n+1}{p}] = [\frac{n}{p}]](/forum/ext/geomar/texintegr/latexrender/pictures/70d2c011da5256fd0212d8d92301e8ed.png)
επειδή όλοι πρώτοι που είναι μικρότεροι η ίσοι του

δεν διαιρούν τον

, επειδή ο

είναι πρώτος από υπόθεση.
Οπότε
![\sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n}( [\frac{n+1}{p}]) +1 \sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n}( [\frac{n+1}{p}]) +1](/forum/ext/geomar/texintegr/latexrender/pictures/cb78e7d57a6a68b786894f8bfa870009.png)
=
![\sum_{p \leq n} [\frac{n}{p}] +1 \sum_{p \leq n} [\frac{n}{p}] +1](/forum/ext/geomar/texintegr/latexrender/pictures/1a51e2d795ad0a0bf8f28c9fbad226f7.png)

και η (1) ισχύει.
Αν ο

δεν είναι πρώτος τότε
![\sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] = \sum_{p \mid n+1} [\frac{n+1}{p}] + \sum_{p \nmid n+1 } [\frac{n+1}{p}] \sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] = \sum_{p \mid n+1} [\frac{n+1}{p}] + \sum_{p \nmid n+1 } [\frac{n+1}{p}]](/forum/ext/geomar/texintegr/latexrender/pictures/f9c61e4bccf2e96dfac10cd556145a0c.png)
=
![\sum_{p \mid n+1}([\frac{n}{p}]+1 ) + \sum_{p \nmid n+1} [\frac{n}{p}] \sum_{p \mid n+1}([\frac{n}{p}]+1 ) + \sum_{p \nmid n+1} [\frac{n}{p}]](/forum/ext/geomar/texintegr/latexrender/pictures/bfb9f6c012d8e4b3926b398fc1a0ae21.png)
![= \sum_{p \leq n}[\frac{n}{p}] + \omega(n+1) = \sum_{p \leq n}[\frac{n}{p}] + \omega(n+1)](/forum/ext/geomar/texintegr/latexrender/pictures/37b90aed000b4bb83e7e77ded9aca74b.png)
το οποίο σημαίνει ότι ισχύει η (1) για τον

και το συμπέρασμα έπεται.
 ο ελάχιστος αριθμός
ο ελάχιστος αριθμός  ώστε κάθε αρκετά μεγάλος αριθμός να γράφεται ως άθροιμα
ώστε κάθε αρκετά μεγάλος αριθμός να γράφεται ως άθροιμα  μη αρνητικών κύβων.
μη αρνητικών κύβων.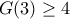 .
. είναι ένα από τα μεγαλύτερα ανοιχτά προβλήματα της Προσθετικής Θεωρίας Αριθμών.
είναι ένα από τα μεγαλύτερα ανοιχτά προβλήματα της Προσθετικής Θεωρίας Αριθμών. . Οι περισσότεροι μαθηματικοί πιστεύουν ότι
. Οι περισσότεροι μαθηματικοί πιστεύουν ότι  .
.
 ;
; , τότε έστω ένας πρώτο
, τότε έστω ένας πρώτο  με
με  και από το θεώρημα του Dirichlet ξέρουμε ότι υπάρχουν άπειροι τέτοιοι πρώτοι. Τότε από υπόθεση ισχύει
και από το θεώρημα του Dirichlet ξέρουμε ότι υπάρχουν άπειροι τέτοιοι πρώτοι. Τότε από υπόθεση ισχύει  . Εύκολα δείχνουμε ότι
. Εύκολα δείχνουμε ότι  . Παίρνοντας όλους τους πιθανούς συνδυασμούς βλέπουμε ότι
. Παίρνοντας όλους τους πιθανούς συνδυασμούς βλέπουμε ότι  . Άρα
. Άρα  .
. στους φυσικούς είναι η
στους φυσικούς είναι η  .
. ο ελάχιστος αριθμός
ο ελάχιστος αριθμός  .
. .
.
 .
. καθώς
καθώς  .
. . Η συνάρτηση
. Η συνάρτηση  είναι το πλήθος των πρώτων διαιρετών του
είναι το πλήθος των πρώτων διαιρετών του  .
.
 και
και  .
.![\frac{n}{p} = [\frac{n}{p}] + \frac{n mod p}{p} \frac{n}{p} = [\frac{n}{p}] + \frac{n mod p}{p}](/forum/ext/geomar/texintegr/latexrender/pictures/a0cbd2d008ddc132ae2757ab493cdec3.png) , όπου
, όπου  το υπόλοιπο της ευκλείδειας διαίρεσης του
το υπόλοιπο της ευκλείδειας διαίρεσης του ![n \sum_{p \leq n} \frac{1}{p} = \sum_{p \leq n} [\frac{n}{p}] + \sum_{p \leq n} \frac{nmodp}{p} n \sum_{p \leq n} \frac{1}{p} = \sum_{p \leq n} [\frac{n}{p}] + \sum_{p \leq n} \frac{nmodp}{p}](/forum/ext/geomar/texintegr/latexrender/pictures/113a45abe8dce59cdd25bcde8288b07b.png) , οπότε
, οπότε![\sum_{p \leq n} \frac{1}{p} = \frac{1}{n}\sum_{p \leq n} [\frac{n}{p}] + \frac{1}{n}\sum_{p \leq n} \frac{nmodp}{p} \sum_{p \leq n} \frac{1}{p} = \frac{1}{n}\sum_{p \leq n} [\frac{n}{p}] + \frac{1}{n}\sum_{p \leq n} \frac{nmodp}{p}](/forum/ext/geomar/texintegr/latexrender/pictures/0dd6bf07b9abe3994e09b626f56b1345.png) .
.
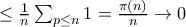 καθώς
καθώς ![\sum_{p \leq n} [\frac{n}{p}] = \sum_{k=1}^{n} \omega(k) \sum_{p \leq n} [\frac{n}{p}] = \sum_{k=1}^{n} \omega(k)](/forum/ext/geomar/texintegr/latexrender/pictures/bfb78f9d7c8592daf9505f1969926766.png) (1). Θα χρησιμοποιήσουμε μαθηματική επαγωγή.
(1). Θα χρησιμοποιήσουμε μαθηματική επαγωγή. έχουμε ότι η (1) ισχύει.
έχουμε ότι η (1) ισχύει. είναι πρώτος τότε
είναι πρώτος τότε ![\sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] +1 \sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] +1](/forum/ext/geomar/texintegr/latexrender/pictures/60d1cc496fa3e9e2ea4fe45562ab19f6.png) .
.![[\frac{n+1}{p}] = [\frac{n}{p}] [\frac{n+1}{p}] = [\frac{n}{p}]](/forum/ext/geomar/texintegr/latexrender/pictures/70d2c011da5256fd0212d8d92301e8ed.png) επειδή όλοι πρώτοι που είναι μικρότεροι η ίσοι του
επειδή όλοι πρώτοι που είναι μικρότεροι η ίσοι του ![\sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n}( [\frac{n+1}{p}]) +1 \sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n}( [\frac{n+1}{p}]) +1](/forum/ext/geomar/texintegr/latexrender/pictures/cb78e7d57a6a68b786894f8bfa870009.png) =
= ![\sum_{p \leq n} [\frac{n}{p}] +1 \sum_{p \leq n} [\frac{n}{p}] +1](/forum/ext/geomar/texintegr/latexrender/pictures/1a51e2d795ad0a0bf8f28c9fbad226f7.png)
 και η (1) ισχύει.
και η (1) ισχύει.![\sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] = \sum_{p \mid n+1} [\frac{n+1}{p}] + \sum_{p \nmid n+1 } [\frac{n+1}{p}] \sum_{p \leq n+1} [\frac{n+1}{p}] = \sum_{p \leq n} [\frac{n+1}{p}] = \sum_{p \mid n+1} [\frac{n+1}{p}] + \sum_{p \nmid n+1 } [\frac{n+1}{p}]](/forum/ext/geomar/texintegr/latexrender/pictures/f9c61e4bccf2e96dfac10cd556145a0c.png) =
= ![\sum_{p \mid n+1}([\frac{n}{p}]+1 ) + \sum_{p \nmid n+1} [\frac{n}{p}] \sum_{p \mid n+1}([\frac{n}{p}]+1 ) + \sum_{p \nmid n+1} [\frac{n}{p}]](/forum/ext/geomar/texintegr/latexrender/pictures/bfb9f6c012d8e4b3926b398fc1a0ae21.png)
![= \sum_{p \leq n}[\frac{n}{p}] + \omega(n+1) = \sum_{p \leq n}[\frac{n}{p}] + \omega(n+1)](/forum/ext/geomar/texintegr/latexrender/pictures/37b90aed000b4bb83e7e77ded9aca74b.png) το οποίο σημαίνει ότι ισχύει η (1) για τον
το οποίο σημαίνει ότι ισχύει η (1) για τον  , έχουμε ότι κάθε πολλαπλάσιο του
, έχουμε ότι κάθε πολλαπλάσιο του  γράφεται στη μορφή
γράφεται στη μορφή  .
. φυσικό αριθμό ισχύει
φυσικό αριθμό ισχύει  .
.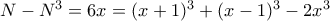 , οπότε
, οπότε , το οποίο αποδεικνύει ότι
, το οποίο αποδεικνύει ότι