 ώστε κάθε φυσικός αριθμός
ώστε κάθε φυσικός αριθμός  να γράφεται στη μορφή
να γράφεται στη μορφή  για κάποιους φυσικούς
για κάποιους φυσικούς  .
.Συντονιστής: nkatsipis
 ώστε κάθε φυσικός αριθμός
ώστε κάθε φυσικός αριθμός  να γράφεται στη μορφή
να γράφεται στη μορφή  για κάποιους φυσικούς
για κάποιους φυσικούς  .
.

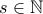 τότε υπάρχει
τότε υπάρχει  ώστε κάθε φυσικός
ώστε κάθε φυσικός  γράφεται στη μορφή
γράφεται στη μορφή  .
.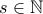 τότε υπάρχει
τότε υπάρχει  ώστε κάθε φυσικός
ώστε κάθε φυσικός  γράφεται στη μορφή
γράφεται στη μορφή  , το οποίο το απέδειξε ο Hilbert.
, το οποίο το απέδειξε ο Hilbert. και τέτοια αλλά νομίζω ότι είναι ανοιχτό πρόβλημα.
και τέτοια αλλά νομίζω ότι είναι ανοιχτό πρόβλημα. ώστε κάθε αρκετά μεγάλος φυσικός να είναι άθροισμα
ώστε κάθε αρκετά μεγάλος φυσικός να είναι άθροισμα  κύβων.
κύβων.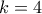 .
.Τι γίνεται αν θέλουμε να βρούμε το ελάχιστοΜάρκος Βασίλης έγραψε: ↑Κυρ Μαρ 22, 2020 9:29 pmΝομίζω ότι με την υπόδειξη είναι αρκετά εύκολο, αφού για κάθε άρτιο χρειαζόμαστε 3 και για κάθε περιττό 2 τετράγωνα ενώ για το 6 δεν υπάρχει βραχύτερη γραφή από την:
Πράγματι, δεν μπορούμε να πάρουμε το 6 ως διαφορά δύο τετραγώνων, αφού διαδοχικά τετράγωνα διαφέρουν κατά περιττό και για τετράγωνα μεγαλύτερα του 9 οι διαφορές είναι μεγαλύτερες του 7.
Θυμίζει, στα πολύ απλά του, το θεώρημα του Lagrange η παραπάνω άσκηση - αν και το θεώρημα έχει αρκετά πιο περίτεχνη απόδειξη.
 ώστε κάθε αρκετά μεγάλος αριθμός να γράφεται
ώστε κάθε αρκετά μεγάλος αριθμός να γράφεται 
Για να κάνω την αρχή, από το θεώρημα του Lagrange,stranger έγραψε: ↑Δευ Μαρ 23, 2020 4:47 amΤι γίνεται αν θέλουμε να βρούμε το ελάχιστοΜάρκος Βασίλης έγραψε: ↑Κυρ Μαρ 22, 2020 9:29 pmΝομίζω ότι με την υπόδειξη είναι αρκετά εύκολο, αφού για κάθε άρτιο χρειαζόμαστε 3 και για κάθε περιττό 2 τετράγωνα ενώ για το 6 δεν υπάρχει βραχύτερη γραφή από την:
Πράγματι, δεν μπορούμε να πάρουμε το 6 ως διαφορά δύο τετραγώνων, αφού διαδοχικά τετράγωνα διαφέρουν κατά περιττό και για τετράγωνα μεγαλύτερα του 9 οι διαφορές είναι μεγαλύτερες του 7.
Θυμίζει, στα πολύ απλά του, το θεώρημα του Lagrange η παραπάνω άσκηση - αν και το θεώρημα έχει αρκετά πιο περίτεχνη απόδειξη.ώστε κάθε αρκετά μεγάλος αριθμός να γράφεται

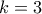 ή
ή 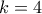 .
.
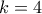 . Από την απόδειξή σου έχουμε ότι
. Από την απόδειξή σου έχουμε ότι  . Επίσης μπορεί να ισχύει
. Επίσης μπορεί να ισχύει  .
.Ναι, σωστά, για κάποιον λόγο αγνόησα τα
 και τα έκανα
και τα έκανα  - εξ ου και η αναφορά στον Lagrange.
- εξ ου και η αναφορά στον Lagrange.
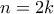 σε αθροίσματα διαδοχικών περιττών αριθμών έχουν ως εξής:
σε αθροίσματα διαδοχικών περιττών αριθμών έχουν ως εξής: , αν
, αν 
 , αν
, αν 
 , αν
, αν  , για
, για 
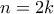 σε άθροισμα διαδοχικών περιττών πρέπει να ισχύει
σε άθροισμα διαδοχικών περιττών πρέπει να ισχύει  για κάποιο
για κάποιο  - για την δουλειά που εμείς θέλουμε, θα πρέπει και όλοι οι προσθετέοι του αθροίσματος να είναι θετικοί.
- για την δουλειά που εμείς θέλουμε, θα πρέπει και όλοι οι προσθετέοι του αθροίσματος να είναι θετικοί.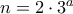 ,
, 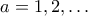 έχουμε
έχουμε  το οποίο είναι περιττός για κάθε τιμή του
το οποίο είναι περιττός για κάθε τιμή του  - ως γινόμενο περιττών - επομένως δεν ισχύει η συνθήκη
- ως γινόμενο περιττών - επομένως δεν ισχύει η συνθήκη  για κανένα
για κανένα  .
.
 έχουν άρτιο εκθέτη.
έχουν άρτιο εκθέτη.Άρα, για
 περιττό, ο
περιττό, ο  μας κάνει και πάλι.
μας κάνει και πάλι.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες