 θετικών ακέραιων κύβων είναι ο
θετικών ακέραιων κύβων είναι ο 
Συντονιστής: nkatsipis
 θετικών ακέραιων κύβων είναι ο
θετικών ακέραιων κύβων είναι ο 

 τέλειος άρτιος και έστω
τέλειος άρτιος και έστω  τότε.........
τότε.........

 and
and  τότε:
τότε:

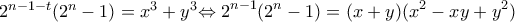

 τότε
τότε  που είναι προφανές αδύνατο.
που είναι προφανές αδύνατο. τότε έχουμε
τότε έχουμε  περίπτωσης:
περίπτωσης:
 Αν
Αν 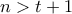 τότε:Από την πρώτη έχω ένας άρτιος και ο άλλος περιττός ενώ από την δεύτερη και οι δύο περιττή.Αδυνατη.
τότε:Από την πρώτη έχω ένας άρτιος και ο άλλος περιττός ενώ από την δεύτερη και οι δύο περιττή.Αδυνατη. Αν
Αν 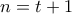 έχω την:
έχω την:  που έχει μοναδική λύση την
που έχει μοναδική λύση την 
 and
and 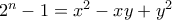
 Αν
Αν  τότε:
τότε: η τα αντίστροφα όμως τότε:
η τα αντίστροφα όμως τότε:
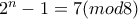
 Αν
Αν  Εξετάζω με το χέρι τής
Εξετάζω με το χέρι τής  .....
.....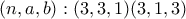
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες