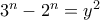 .
.Σημείωση: Για να είμαι δίκαιος είναι εμπνευσμένη από μια παρόμοια άσκηση στην ομάδα 'Μαθηματικο Εργαστήρι' στο facebook του κ. Κυριακοπουλου.
Συντονιστής: nkatsipis
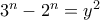 .
.Πολύ σωστά!!!
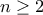 , τότε δουλεύοντας
, τότε δουλεύοντας  καταλαβαίνουμε ότι
καταλαβαίνουμε ότι 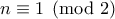 . Έστω
. Έστω  και
και 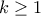 . Τότε παίρνοντας την εξίσωση
. Τότε παίρνοντας την εξίσωση 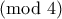 βγάζουμε ότι
βγάζουμε ότι 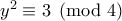 που είναι άτοπο.
που είναι άτοπο. που ικανοποιούν την εξήσωση:
που ικανοποιούν την εξήσωση: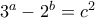
Αν
 τότε προφανώς πρέπει
τότε προφανώς πρέπει  , που δίνει την λύση
, που δίνει την λύση  .
. , τότε
, τότε 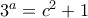 και άρα αν
και άρα αν  παίρνουμε άτοπο
παίρνουμε άτοπο 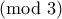 . Άρα έχουμε πάλι μόνο τη μηδενική λύση
. Άρα έχουμε πάλι μόνο τη μηδενική λύση τότε προκύπτει μόνο η μηδενική λύση.
τότε προκύπτει μόνο η μηδενική λύση. . Αν
. Αν  τότε
τότε  , και αφού ο
, και αφού ο  είναι περιττός, έχουμε
είναι περιττός, έχουμε 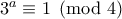 , συνεπώς ο
, συνεπώς ο  είναι άρτιος, έστω
είναι άρτιος, έστω 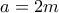 . Τότε,
. Τότε, 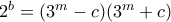 .
.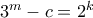 ,
, 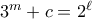 με
με  φυσικούς με
φυσικούς με  . Αν
. Αν 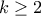 τότε είναι
τότε είναι 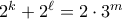 , άτοπο
, άτοπο  . Άρα
. Άρα 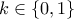 .
.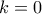 , τότε
, τότε 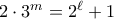 , άτοπο. Αν
, άτοπο. Αν  , τότε
, τότε  , οπότε από Catalan Conjecture πρέπει
, οπότε από Catalan Conjecture πρέπει  ή
ή  (εντάξει
(εντάξει  με
με  πρέπει
πρέπει 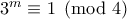 , δηλαδή
, δηλαδή  άρτιος, οπότε αν
άρτιος, οπότε αν  είναι
είναι 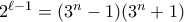 , και το
, και το  δεν μπορεί να είναι δύναμη του
δεν μπορεί να είναι δύναμη του  για
για  , καθώς
, καθώς  ή
ή  )
)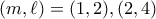 , και προκύπτουν οι λύσεις
, και προκύπτουν οι λύσεις  .
. , όπου έχουμε
, όπου έχουμε  . Με
. Με  , είναι
, είναι 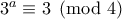 , άρα ο
, άρα ο  είναι περιττός, έστω
είναι περιττός, έστω 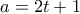 , οπότε έχουμε
, οπότε έχουμε 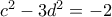 , με
, με 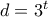 .
. , και της οποίας η γενική λύση
, και της οποίας η γενική λύση 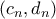 δίνεται από τις ακολουθίες
δίνεται από τις ακολουθίες 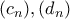 με
με  και
και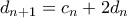 (με
(με 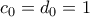 ).
).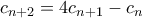 και
και  .
.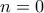 ισχύουν οι πιο πάνω. Έστω ότι ισχύουν για κάθε
ισχύουν οι πιο πάνω. Έστω ότι ισχύουν για κάθε 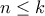 . Θα τις δείξουμε για
. Θα τις δείξουμε για  . Πράγματι,
. Πράγματι,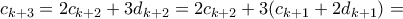
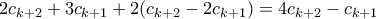 , και
, και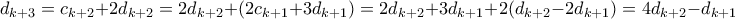 , και η απόδειξη ολοκληρώθηκε
, και η απόδειξη ολοκληρώθηκε 
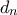 με
με  και
και 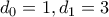 , και ψάχνουμε ποιοι όροι της είναι δυνάμεις του
, και ψάχνουμε ποιοι όροι της είναι δυνάμεις του  .
.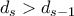 τότε
τότε 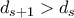 . Για το επαγωγικό βήμα είναι
. Για το επαγωγικό βήμα είναι  ). Επίσης οι δύο πρώτοι όροι είναι δυνάμεις του
). Επίσης οι δύο πρώτοι όροι είναι δυνάμεις του  . Άρα και
. Άρα και  για
για  . Οπότε θα αναζητήσουμε δυνάμεις του
. Οπότε θα αναζητήσουμε δυνάμεις του  που είναι
που είναι 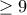 .
. προκύπτει:
προκύπτει: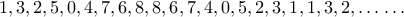
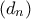 είναι περιοδική
είναι περιοδική  με περίοδο
με περίοδο  . Βλέπουμε λοιπόν ότι οι μόνοι όροι της που είναι πολλαπλάσια του
. Βλέπουμε λοιπόν ότι οι μόνοι όροι της που είναι πολλαπλάσια του  είναι οι
είναι οι 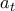 με
με 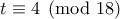 ή
ή 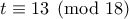 .
.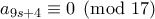 , για κάθε
, για κάθε  .
.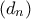
 και προκύπτει
και προκύπτει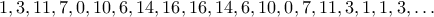
 με περίοδο
με περίοδο  , και εύκολα βλέπουμε ότι είναι
, και εύκολα βλέπουμε ότι είναι  όταν είναι
όταν είναι 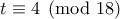 ή
ή 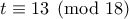 , που δίνει το ζητούμενο.
, που δίνει το ζητούμενο. 
 με
με  .
. και
και  , οπότε και
, οπότε και 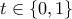 . Αν
. Αν  είναι
είναι  , και αν
, και αν  είναι
είναι 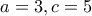 .
.
Ομολογώ πως δεν έχω ολοκληρωμένη λύση (προσπάθησα χωρίς Πέλλ, και σας συνιστώ να μην το κάνετε κι εσείς
 , τότε
, τότε 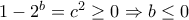 , άρα
, άρα  και
και  .
. , τότε
, τότε 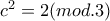 , άτοπο, αφού το
, άτοπο, αφού το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  .
.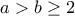 .
. περιττός, τότε έχω ότι
περιττός, τότε έχω ότι 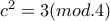 , άτοπο, αφού το
, άτοπο, αφού το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο 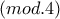 , επομένως
, επομένως 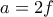 .
.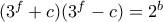 .
.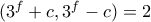 και
και 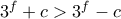 , οπότε θα έχουμε το σύστημα:
, οπότε θα έχουμε το σύστημα: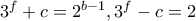 ♦.
♦.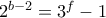 .
.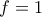 , τότε
, τότε  , ενώ αν
, ενώ αν 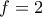 , τότε
, τότε 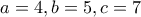 .
.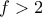 . Τότε όμως από το Θεώρημα
. Τότε όμως από το Θεώρημα  υπάρχει
υπάρχει 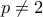 , τέτοιος ώστε
, τέτοιος ώστε 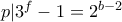 , άτοπο.
, άτοπο. . Έχουμε την εξίσωση
. Έχουμε την εξίσωση  .
. περιττοί, οπότε γράφουμε
περιττοί, οπότε γράφουμε 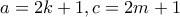 , και η εξίσωση γίνεται:
, και η εξίσωση γίνεται: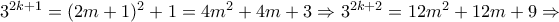
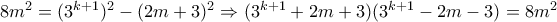 .
. , οπότε οι περιπτώσεις είναι πολλές. Αφού τις εξετάσουμε και τις απορρίψουμε μία προς μία, μένουν δύο που δυστυχώς
, οπότε οι περιπτώσεις είναι πολλές. Αφού τις εξετάσουμε και τις απορρίψουμε μία προς μία, μένουν δύο που δυστυχώς Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες