 και
και  . Το τμήμα
. Το τμήμα 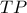
με άκρα στα δύο τόξα κινείται , παραμένοντας παράλληλο προς την
 .
. Οι ημιευθείες
 τέμνονται στο
τέμνονται στο  . Υπολογίστε το :
. Υπολογίστε το :  .
.Συντονιστής: gbaloglou
 και
και  . Το τμήμα
. Το τμήμα 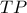
 .
.  τέμνονται στο
τέμνονται στο  . Υπολογίστε το :
. Υπολογίστε το :  .
.Έστω
 και
και  . Τότε θα εύκολα διαπιστώνουμε ότι:
. Τότε θα εύκολα διαπιστώνουμε ότι: 
 Από τον νόμο των ημιτόνων στο τρίγωνο
Από τον νόμο των ημιτόνων στο τρίγωνο  θα έχουμε:
θα έχουμε: 
 και
και 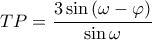 . Θέτουμε
. Θέτουμε ![\sin \omega =t,t\in \left[ 0,1 \right] \sin \omega =t,t\in \left[ 0,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ca9ef3e64a3c1f357361845d6cd3dc4d.png) οπότε
οπότε  ,
,  και
και  (αφού οι γωνίες είναι οξείες) , έτσι έχουμε:
(αφού οι γωνίες είναι οξείες) , έτσι έχουμε: 

 και
και  οπότε με αφαίρεση κατά μέλη παίρνουμε:
οπότε με αφαίρεση κατά μέλη παίρνουμε: 

 . Από Τον τύπο
. Από Τον τύπο  θα έχουμε:
θα έχουμε:  και
και  οπότε η σχέση
οπότε η σχέση  και με την βοήθεια της σχέσης
και με την βοήθεια της σχέσης  και θέτοντας
και θέτοντας  δίνει τη συνάρτηση
δίνει τη συνάρτηση ![f\left( x \right)=\dfrac{{{\left( 3\sqrt{1-\dfrac{4}{9}x}-2\sqrt{1-x} \right)}^{2}}}{2\left( \sqrt{\dfrac{1-\sqrt{1-x}}{1+\sqrt{1-x}}}-\sqrt{\dfrac{1-\sqrt{1-\dfrac{4}{9}x}}{1+\sqrt{1-\dfrac{4}{9}x}}} \right)},x\in \left[ 0,1 \right] f\left( x \right)=\dfrac{{{\left( 3\sqrt{1-\dfrac{4}{9}x}-2\sqrt{1-x} \right)}^{2}}}{2\left( \sqrt{\dfrac{1-\sqrt{1-x}}{1+\sqrt{1-x}}}-\sqrt{\dfrac{1-\sqrt{1-\dfrac{4}{9}x}}{1+\sqrt{1-\dfrac{4}{9}x}}} \right)},x\in \left[ 0,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e23cddde696df6e90ed9c560d8dfa3c0.png) της οποίας η γραφική παράσταση και το ακρότατο φαίνεται πιο κάτω .
Σημείωση: Η αναλυτική μελέτη της εν λόγω συνάρτησης αφήνεται για τον Εισηγητή ή όποιον άλλον καλό φίλο δεν έχει «δουλειές»
της οποίας η γραφική παράσταση και το ακρότατο φαίνεται πιο κάτω .
Σημείωση: Η αναλυτική μελέτη της εν λόγω συνάρτησης αφήνεται για τον Εισηγητή ή όποιον άλλον καλό φίλο δεν έχει «δουλειές» Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες