Α) Αυτά που περιέχονται στα σχολικά βιβλία ( και τα : διχοτόμων , διαμέσων , τεμνόμενων χορδών ) .
Β) Αυτά που έχουν συνάφεια με το σχολικό ( π.χ είναι απαιτητικές ασκήσεις ) , όπως τα :
Μενελάου , Πτολεμαίου , Stewart , Van Aubel , Nagel , ευθεία Simson , κύκλος Euler κ.λ.π.
Γ) Δυσκολότερα θεωρήματα , τα οποία ο μέσος μαθητής πιθανότατα δεν θα ακούσει ποτέ .
Συλλογή τέτοιων θεωρημάτων δείτε στην έξοχη εργασία του parmenides , εδώ .
Προτείνω ως τέταρτη ομάδα , τις προτάσεις εκείνες , οι οποίες χρησιμοποιούνται στον ιστότοπο mathematica ,
τόσο συχνά , ώστε να επέχουν πλέον θέσεις θεωρημάτων .
 Η λίστα αυτή θα έχει ασφαλώς στην πρώτη θέση το "κανονικό" Θεώρημα Κούτρα .
Η λίστα αυτή θα έχει ασφαλώς στην πρώτη θέση το "κανονικό" Θεώρημα Κούτρα .Ακολουθούν κάποιες προτάσεις με τις παραπομπές τους :
 Αν
Αν  σημείο εσωτερικό γωνίας
σημείο εσωτερικό γωνίας  και τμήμα
και τμήμα  με άκρα στις πλευρές της γωνίας
με άκρα στις πλευρές της γωνίαςδιέρχεται από το
 , τότε το
, τότε το  ελαχιστοποιείται όταν :
ελαχιστοποιείται όταν :  . Εδώ
. Εδώ Σε τρίγωνο με :
Σε τρίγωνο με :  , ισχύει :
, ισχύει :  . εδώ
. εδώΗ λίστα αυτή λογικά θα συγκεντρώσει αρκετές ακόμα προτάσεις ( ίσως
 με
με  ) . Συνεχίζεται ...
) . Συνεχίζεται ...
 Αν το παράλληλο προς τις βάσεις του τραπεζίου , τμήμα
Αν το παράλληλο προς τις βάσεις του τραπεζίου , τμήμα  σε τμήματα :
σε τμήματα : και
και  , τότε είναι :
, τότε είναι :  . Αποδείξεις υπάρχουν στο
. Αποδείξεις υπάρχουν στο  είναι παραλληλόγραμμα .
είναι παραλληλόγραμμα . είναι όμοια.
είναι όμοια.  με
με  .
.

 και
και 

 . Τότε με
. Τότε με  και ομοίως από
και ομοίως από  ¨. Με πρόσθεση κατά μέλη των σχέσεων
¨. Με πρόσθεση κατά μέλη των σχέσεων  προκύπτει ότι
προκύπτει ότι 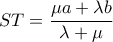

 ισχύει η ισοδυναμία :
ισχύει η ισοδυναμία :  .
. .
.

 , που ισχύει.
, που ισχύει. . Έστω
. Έστω 
 (1)
(1) (2),
(2), 

 , εφόσον
, εφόσον 