 να εγγραφεί το μεγίστου εμβαδού τρίγωνο
να εγγραφεί το μεγίστου εμβαδού τρίγωνο  , στο οποίο να είναι
, στο οποίο να είναι  .
.Συντονιστής: gbaloglou
Μη αναγνωσμένη δημοσίευση από KARKAR » Πέμ Μάιος 06, 2021 9:10 am
 να εγγραφεί το μεγίστου εμβαδού τρίγωνο
να εγγραφεί το μεγίστου εμβαδού τρίγωνο  , στο οποίο να είναι
, στο οποίο να είναι  .
.Μη αναγνωσμένη δημοσίευση από george visvikis » Πέμ Μάιος 06, 2021 11:11 am
Προφανώς
 Αρκεί να υπολογίσω το τμήμα
Αρκεί να υπολογίσω το τμήμα  Το
Το  είναι το σημείο τομής
είναι το σημείο τομής  με τον Απολλώνιο, για τα σημεία
με τον Απολλώνιο, για τα σημεία  του οποίου, ισχύει
του οποίου, ισχύει 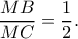

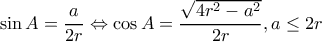
 Νόμος συνημιτόνου,
Νόμος συνημιτόνου, 



 όπου με τη βοήθεια παραγώγων βρίσκω ότι για
όπου με τη βοήθεια παραγώγων βρίσκω ότι για  παρουσιάζει μέγιστη τιμή ίση με
παρουσιάζει μέγιστη τιμή ίση με 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off