 . Το
. Το  κινείται επί της
κινείται επί της  . Το
. Το  εφάπτεται στο "βόρειο"
εφάπτεται στο "βόρειο" ημικύκλιο διαμέτρου
 . Υπολογίστε το μέγιστο του
. Υπολογίστε το μέγιστο του  και βρείτε την τότε θέση του σημείου
και βρείτε την τότε θέση του σημείου  .
.Συντονιστής: gbaloglou
 . Το
. Το  κινείται επί της
κινείται επί της  . Το
. Το  εφάπτεται στο "βόρειο"
εφάπτεται στο "βόρειο"  . Υπολογίστε το μέγιστο του
. Υπολογίστε το μέγιστο του  και βρείτε την τότε θέση του σημείου
και βρείτε την τότε θέση του σημείου  .
. θεωρώ τμήμα
θεωρώ τμήμα  τέτοιο ώστε
τέτοιο ώστε 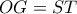 και συγκρίνω τα εμβαδά
και συγκρίνω τα εμβαδά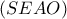 ,
,  για θέση του
για θέση του  πάνω ή κάτω του
πάνω ή κάτω του  .
. διατρέχει από το
διατρέχει από το  στο
στο  το
το  διατρέχει από το
διατρέχει από το  στο
στο  .
.
 τότε
τότε  .
.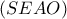 αυξάνεται γραμμικά από το
αυξάνεται γραμμικά από το  στο
στο  ,
,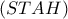 θα μεγιστοποιηθεί όταν το
θα μεγιστοποιηθεί όταν το  ταυτιστεί με το
ταυτιστεί με το  .
. σε κατάλληλα διαμορφωμένο σχήμα όπου
σε κατάλληλα διαμορφωμένο σχήμα όπου  ,
, ,
,  και
και  . Επιλύοντας τότε τις κάτωθι εξισώσεις
. Επιλύοντας τότε τις κάτωθι εξισώσεις
 από όπου
από όπου .
.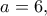 το ίδιο αποτέλεσμα με τον Νίκο Φραγκάκη, ενώ αρχικά
το ίδιο αποτέλεσμα με τον Νίκο Φραγκάκη, ενώ αρχικά  Ακόμα την προσπαθώ...
Ακόμα την προσπαθώ...Ίσως δεν βλέπω κάτι. Το δικό μου συμπέρασμα από τιςnickchalkida έγραψε: ↑Τρί Αύγ 11, 2020 12:17 pm
...
Παρόμοια αποδεικνύεται ότι γιατότε
.
Αλλά το εμβαδό τουαυξάνεται γραμμικά από το
στο
,
άρα τοθα μεγιστοποιηθεί όταν το
ταυτιστεί με το
.


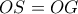 τότε
τότε 
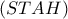 .
. ;
;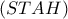 . Αύξουσα για
. Αύξουσα για  πάνω από το
πάνω από το  και φθίνουσα για κάτω (αλλά και πάλι ελλειπές).
και φθίνουσα για κάτω (αλλά και πάλι ελλειπές).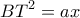 και με νόμο συνημιτόνων στα τρίγωνα
και με νόμο συνημιτόνων στα τρίγωνα  και απαλοιφή του
και απαλοιφή του  παίρνω
παίρνω  Στη συνέχεια με νόμο συνημιτόνου στο
Στη συνέχεια με νόμο συνημιτόνου στο  και επειδή
και επειδή 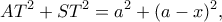 βρίσκω
βρίσκω 
 έχουμε μέγιστο εμβαδόν
έχουμε μέγιστο εμβαδόν 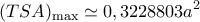
.nickchalkida έγραψε: ↑Τρί Αύγ 11, 2020 6:37 pmΔιαφωνούμε ότι το μέγιστο επιτυγχάνεται για;
Για την παρατήρηση του κυρίου Μιχάλη να πω ότι έχει δίκιο. Η φράση "αυξάνεται γραμμικά"
έκρυψε με πολύ λίγα λόγια το προφανές από τη δημιουργία του σχήματος στο Geogebra
για την μεταβολή του εμβαδού. Αύξουσα για
πάνω από το
και φθίνουσα για κάτω (αλλά και πάλι ελλειπές).
Μια αυστηρή απόδειξη θα χαλούσε αυτά που ήθελα να δείξω.
.Mihalis_Lambrou έγραψε: ↑Τρί Αύγ 11, 2020 3:48 pmΔυσκολεύομαι να καταλάβω το εξής βήμα (από το "άρα" και κάτω):
Δεν βλέπω πώς βγαίνει το συμπέρασμα ότι τότε θα μεγιστοποιηθεί τοnickchalkida έγραψε: ↑Τρί Αύγ 11, 2020 12:17 pm
...
Παρόμοια αποδεικνύεται ότι γιατότε
.
Αλλά το εμβαδό τουαυξάνεται γραμμικά από το
στο
,
άρα τοθα μεγιστοποιηθεί όταν το
ταυτιστεί με το
.
.
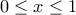 ισχύει
ισχύει 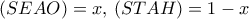 . Παρατηρούμε ότι για
. Παρατηρούμε ότι για  ισχύει
ισχύει  καθώς ισοδυναμεί με το αληθές
καθώς ισοδυναμεί με το αληθές  . Επίσης για
. Επίσης για  ισχύει
ισχύει  καθώς ισοδυναμεί με το αληθές
καθώς ισοδυναμεί με το αληθές  .
. 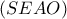 αυξάνει με το
αυξάνει με το  . Όμως η
. Όμως η  δεν λαμβάνει το μέγιστό της όταν
δεν λαμβάνει το μέγιστό της όταν  (το λαμβάνει στο
(το λαμβάνει στο  ), όπως ισχυρίζεται το παραπάνω επιχείρημα.
), όπως ισχυρίζεται το παραπάνω επιχείρημα.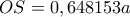 , που είναι διαφορετική από την απάντηση του Νίκου (nickchalkida)
, που είναι διαφορετική από την απάντηση του Νίκου (nickchalkida) 
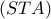 μπορεί να γίνει με καθαρά Μαθηματικά. Η παράσταση είναι τεράστια και μόνο με λογισμικό (και άρα με τα σφάλματα που μπορεί να ελλοχεύουν) μπορούμε να βγάλουμε κάποια τιμή.
μπορεί να γίνει με καθαρά Μαθηματικά. Η παράσταση είναι τεράστια και μόνο με λογισμικό (και άρα με τα σφάλματα που μπορεί να ελλοχεύουν) μπορούμε να βγάλουμε κάποια τιμή. καλό)
καλό)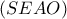 ,
, 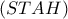 είναι ίσα, παραθέτω παρακάτω
είναι ίσα, παραθέτω παρακάτω Η μωβ γραμμή παριστά την μεταβολή του εμβαδού
Η μωβ γραμμή παριστά την μεταβολή του εμβαδού 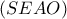 η με καφέ
η με καφέ 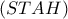 η οποία έχει κορυφή στο
η οποία έχει κορυφή στο  .
. Το
Το  διατρέχει από το
διατρέχει από το  στο
στο  .
.
 είναι το σημείο της
είναι το σημείο της  κατά το οποίο η
κατά το οποίο η 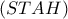 μεγιστοποιείται.
μεγιστοποιείται.
 είναι το σημείο της
είναι το σημείο της  κατά το οποίο
κατά το οποίο  και
και  ταυτίζονται.
ταυτίζονται. ,
, , "αριστερά" ή δεξιά του
, "αριστερά" ή δεξιά του  .
. από το
από το  στο
στο  , σε όλες τις περιπτώσεις
, σε όλες τις περιπτώσεις , δηλαδή θέσεις που απορρίπτονταν
, δηλαδή θέσεις που απορρίπτονταν μονότονη συνάρτηση (κόκκινη γραμμή) με μέγιστο
μονότονη συνάρτηση (κόκκινη γραμμή) με μέγιστο  στο
στο 
 γνησίως φθίνουσα (μπλέ γραμμή) τέμνει την την
γνησίως φθίνουσα (μπλέ γραμμή) τέμνει την την  στο
στο 

 και
και  ταυτίζονται.
ταυτίζονται. . Στο πρόβλημα η
. Στο πρόβλημα η 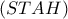 έχει κορυφή
έχει κορυφήΑντί να βελτιώνεται η ασάφεια στην προταθείσα απόδειξη, έχουμε αύξηση των σφαλμάτων. Συγκεκριμένα:nickchalkida έγραψε: ↑Πέμ Αύγ 13, 2020 11:57 am
Έστωμονότονη συνάρτηση (κόκκινη γραμμή) με μέγιστο
στο
ενώ ηγνησίως φθίνουσα (μπλέ γραμμή) τέμνει την την
στο
είναι τέτοια ώστε:
Ισχυρίζομαι ότικαι
ταυτίζονται.
 μονότονη συνάρτηση (κόκκινη γραμμή)" είναι σφάλα εκ παραδρομής και στην θέση του εννοείται "
μονότονη συνάρτηση (κόκκινη γραμμή)" είναι σφάλα εκ παραδρομής και στην θέση του εννοείται " συνεχής συνάρτηση (κόκκινη γραμμή)". Αυτό άλλωστε δηλώνει το σχήμα του Νίκου (nickchalkida). Το συγκεκριμένο το θεωρώ μικρό-διορθώσιμο σφάλμα και αλλού είναι η ένστασή μου. Εδώ:
συνεχής συνάρτηση (κόκκινη γραμμή)". Αυτό άλλωστε δηλώνει το σχήμα του Νίκου (nickchalkida). Το συγκεκριμένο το θεωρώ μικρό-διορθώσιμο σφάλμα και αλλού είναι η ένστασή μου. Εδώ: 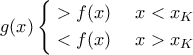
 πρέπει να αντικατασταθεί με την μεταβλητή
πρέπει να αντικατασταθεί με την μεταβλητή  . Αυτό είναι σημαντικό: Αν δείτε την προταθείσα απόδειξη δεν έχει σταθερό αλλά έχει την ανισότητα
. Αυτό είναι σημαντικό: Αν δείτε την προταθείσα απόδειξη δεν έχει σταθερό αλλά έχει την ανισότητα  και, αντίστοιχα,
και, αντίστοιχα,  . Δηλαδή μεταβλητές ποσότητες.
. Δηλαδή μεταβλητές ποσότητες.  . Παίρνουμε
. Παίρνουμε  και
και 
 ισχύει
ισχύει  . Πράγματι, ισοσυναμεί με την
. Πράγματι, ισοσυναμεί με την  , δηλαδή την
, δηλαδή την 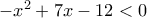 , που αληθεύει καθώς γράφεται ως
, που αληθεύει καθώς γράφεται ως  (αληθές).
(αληθές).  ισχύει
ισχύει  . Πράγματι, όπως πριν, ισοσυναμεί με την αληθή
. Πράγματι, όπως πριν, ισοσυναμεί με την αληθή  (αληθές).
(αληθές). έχουμε
έχουμε  .
. έχει μέγιστο στο
έχει μέγιστο στο  (άμεσο), με άλλα λόγια στο
(άμεσο), με άλλα λόγια στο  έχουμε
έχουμε  . Συμπέρασμα:
. Συμπέρασμα: 
 για
για  και
και  για
για 
 .
.
 τότε
τότε 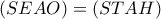
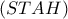 .
. ,
,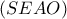 ,
, 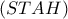 ,
,Επί αυτού δεν υπάρχει αμφιβολία. Είναι ξεκάθαρο ότιnickchalkida έγραψε: ↑Παρ Αύγ 14, 2020 1:05 pm
Το ερώτημα που με απασχολεί είναι αν η μεγιστοποίηση συμβαίνει όταν,
 Στη λύση μου (#7) φαίνεται σαφώς ότι υπάρχει
Στη λύση μου (#7) φαίνεται σαφώς ότι υπάρχει  Πιο συγκεκριμένα είναι
Πιο συγκεκριμένα είναι 
Συμφωνούμε απόλυτα. Δεν είναι μεμπτό να κάνει κανείς λάθος, τουναντίον είναι εποικοδομητικόnickchalkida έγραψε: ↑Τετ Σεπ 23, 2020 9:42 am
Παρ' όλα αυτά νομίζω ότι η παρουσίαση έστω και του λάθους συλλογισμού είναι κάτι
που μπορεί να διδάξει όλους.
Γι' αυτό ακριβώς ρωτάω. Έχει ο θεματοθέτης κάποιο λαγό στο μανίκι του ή μήπως η άσκηση είναι ατυχής (απρόσιτη με ανθρώπινα μέσα);nickchalkida έγραψε: ↑Τετ Σεπ 23, 2020 9:42 amΑυτό που λείπει για το συγκεκριμένο θέμα, είναι μια ακριβής διατύπωση της σωστής λύσης,
αλλά επειδή όπως διαφαίνεται είναι αρκετά επίπονη και μακροσκελής,
Ευγενική υπενθύμιση.Mihalis_Lambrou έγραψε: ↑Τετ Σεπ 23, 2020 2:25 amΘάνο, μια και είσαι ο αρχικός θεματοθέτης στο εδώ θρεντ, μην αμελήσεις να πάρεις θέση για τα παραπάνω. Πέρασε ενάμισος μήνας από το πρώτο ποστ, οπότε τα σχόλιά σου για να μας διαφωτίσεις είναι ευπρόσδεκτα.
Mihalis_Lambrou έγραψε: ↑Τετ Σεπ 23, 2020 11:10 am
Γι' αυτό ακριβώς ρωτάω. Έχει ο θεματοθέτης κάποιο λαγό στο μανίκι του ή μήπως η άσκηση είναι ατυχής (απρόσιτη με ανθρώπινα μέσα);
Μιχάλη , δεν μπόρεσα να αντιληφθώ τι εννοείς με την έκφραση " τα παραπάνω" . Αν πάντως αναφέρεσαι στην προσέγγισηMihalis_Lambrou έγραψε: ↑Τετ Σεπ 23, 2020 2:25 amΘάνο, μια και είσαι ο αρχικός θεματοθέτης στο εδώ θρεντ, μην αμελήσεις να πάρεις θέση για τα παραπάνω.
 , νομίζω ότι το θέμα έχει ήδη διευθετηθεί .
, νομίζω ότι το θέμα έχει ήδη διευθετηθεί .Αν το "προσιτή με ανθρώπινα μέσα" ταυτίζεται με το "χωρίς χρήση λογισμικού" , τότε ασφαλώς δεν έχω τέτοια λύση !Mihalis_Lambrou έγραψε: ↑Τετ Σεπ 23, 2020 11:10 am
Δεν θα ρωτούσα (την άσκηση την έχω λύσει) ...
Έχει ο θεματοθέτης κάποιο λαγό στο μανίκι του ή μήπως η άσκηση είναι ατυχής (απρόσιτη με ανθρώπινα μέσα) ;
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες