 ώστε οι παραβολές
ώστε οι παραβολές  και
και 
να έχουν 4 σημεία τομής.
Γραφικά παρατηρούμε ότι αυτό συμβαίνει για
 . Δεν έχω καταφέρει να το αποδείξω αναλυτικά.
. Δεν έχω καταφέρει να το αποδείξω αναλυτικά.https://www.desmos.com/calculator/7n2kodqvjo
Συντονιστής: gbaloglou
 ώστε οι παραβολές
ώστε οι παραβολές  και
και 
 . Δεν έχω καταφέρει να το αποδείξω αναλυτικά.
. Δεν έχω καταφέρει να το αποδείξω αναλυτικά. η οποία είναι τετάρτου βαθμού, για να έχει 4 πραγματικές ρίζες θα πρέπει η συνάρτηση
η οποία είναι τετάρτου βαθμού, για να έχει 4 πραγματικές ρίζες θα πρέπει η συνάρτηση  να παρουσιάζει τρία τοπικά ακρότατα (τ.ελ-τ.μεγ-τ.ελ) αντίστοιχα η πρώτη παράγωγος θα πρέπει να έχει τρεις πραγματικές ρίζες.
να παρουσιάζει τρία τοπικά ακρότατα (τ.ελ-τ.μεγ-τ.ελ) αντίστοιχα η πρώτη παράγωγος θα πρέπει να έχει τρεις πραγματικές ρίζες.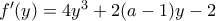 άρα μάλλον θα καταλήξουμε στην μελέτη-διερεύνηση της γνωστής πολυωνυμικής εξίσωσης 3ου βαθμού.
άρα μάλλον θα καταλήξουμε στην μελέτη-διερεύνηση της γνωστής πολυωνυμικής εξίσωσης 3ου βαθμού.dimplak έγραψε: ↑Πέμ Απρ 23, 2020 6:45 pmΚαλησπέρα σας και ευχαριστώ για την άμεση ανταπόκριση.
Όσα προαναφέρατε τα έχω εξάγει και εγώ αλλά με προβληματίζει το γεγονός ότι και να βγάλουμε συνθήκη για τρία ακρότατα δε σημαίνει απαραίτητα
ότι έχει και 4 ρίζες η πολυωνυμική συνάρτηση 4ου βαθμού αλλά πιθανώς να έχει διότι το ακρότατο μπορεί να είναι θετικό αν η συνάρτηση φθίνει και μετά αυξάνει.
Προσπαθώ να προσανατολιστώ γεωμετρικά και με βάση ότι οι δύο παραβολές ανήκουν στην κατηγορία των ορθογώνιων παραβολών, δηλαδή
οι άξονες συμμετρίας τους είναι κάθετοι.
 αν θεωρήσουμε, ότι εφόσον οι παραβολές τέμνονται σε τέσσερα σημεία, θα σχηματίζεται ένα περιγεγράψιμο παραβολικό τετράπλευρο. (βλέπε εδώ). Το κέντρο του εγγεγραμμένου κύκλου είναι σταθερό στην περίπτωσή μας, το σημείο
αν θεωρήσουμε, ότι εφόσον οι παραβολές τέμνονται σε τέσσερα σημεία, θα σχηματίζεται ένα περιγεγράψιμο παραβολικό τετράπλευρο. (βλέπε εδώ). Το κέντρο του εγγεγραμμένου κύκλου είναι σταθερό στην περίπτωσή μας, το σημείο  , που είναι το σημείο τομής των αξόνων των παραβολών. Αυτός ο κύκλος εφπάπτεται και στις δυο παραβολές. Οι εξισώσεις που προκύπτουν μπορεί να δίνουν τα κατάλληλα
, που είναι το σημείο τομής των αξόνων των παραβολών. Αυτός ο κύκλος εφπάπτεται και στις δυο παραβολές. Οι εξισώσεις που προκύπτουν μπορεί να δίνουν τα κατάλληλα  . Δεν έχω κάνει τις πράξεις όμως, μπορεί να οδηγούν σε ισοδύναμα αποτελέσματα με την επίλυση των εξισώσεων, που δεν φαίνονται πολλά υποσχόμενες.
. Δεν έχω κάνει τις πράξεις όμως, μπορεί να οδηγούν σε ισοδύναμα αποτελέσματα με την επίλυση των εξισώσεων, που δεν φαίνονται πολλά υποσχόμενες. .
. ώστε η συνάρτηση αυτή να έχει 4 πραγματικές ρίζες. Ώστε, η δεύτερη παράγωγος (τριώνυμο του
ώστε η συνάρτηση αυτή να έχει 4 πραγματικές ρίζες. Ώστε, η δεύτερη παράγωγος (τριώνυμο του  ) από το Θεώρημα Rolle
) από το Θεώρημα Rolle 
 με ρίζες
με ρίζες
 , με άθροισμα ίσο με
, με άθροισμα ίσο με  και γινόμενο
και γινόμενο  .
. για να έχουμε
για να έχουμε  σημεία τομής έχει σχετικά απλή γεωμετρική διαισθητική ερμηνεία που δίνει εύκολα την απάντηση.
σημεία τομής έχει σχετικά απλή γεωμετρική διαισθητική ερμηνεία που δίνει εύκολα την απάντηση. πρέπει να βρίσκεται αριστερά της μικρότερης ρίζας της εξίσωσης
πρέπει να βρίσκεται αριστερά της μικρότερης ρίζας της εξίσωσης  . Δηλαδή
. Δηλαδή
 ,
,  , την συμμετρική της
, την συμμετρική της  και μελετήσουμε τις συναρτήσεις
και μελετήσουμε τις συναρτήσεις 
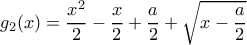
 και την
και την  και να αποκλείσω περιπτώσεις αλλά δεν έχω καταλήξει κάπου.
και να αποκλείσω περιπτώσεις αλλά δεν έχω καταλήξει κάπου.

Ή ίσως θα μπορούσαμε να πάμε κατευθείαν στην γνωστή διερεύνηση λύσεων τεταρτοβάθμιας... Τέλος πάντων, δίνω μια 'γρήγορη' (αλλά όχι πλήρη) αιτιολόγηση για την 'οριακότητα' τηςChristos.N έγραψε: ↑Πέμ Απρ 23, 2020 6:35 pmμάλλον σαν διασταύρωση των ιδεών σου και όχι ως πλήρη λύση τα παρακάτω.
Καταλήγω στηνη οποία είναι τετάρτου βαθμού, για να έχει 4 πραγματικές ρίζες θα πρέπει η συνάρτηση
να παρουσιάζει τρία τοπικά ακρότατα (τ.ελ-τ.μεγ-τ.ελ) αντίστοιχα η πρώτη παράγωγος θα πρέπει να έχει τρεις πραγματικές ρίζες.
Όπουάρα μάλλον θα καταλήξουμε στην μελέτη-διερεύνηση της γνωστής πολυωνυμικής εξίσωσης 3ου βαθμού.
 :
: για το οποίο η
για το οποίο η 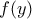 θα έχει διπλή ρίζα, αναζητούμε δηλαδή
θα έχει διπλή ρίζα, αναζητούμε δηλαδή  τέτοια ώστε να ισχύει η ισότητα
τέτοια ώστε να ισχύει η ισότητα



 καταλήγουμε εύκολα στην
καταλήγουμε εύκολα στην  , ενώ η πραγματική ρίζα της
, ενώ η πραγματική ρίζα της 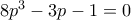 οδηγεί, μέσω
οδηγεί, μέσω  &
&  και
και  , στις
, στις  ,
,  . [Πιθανώς ... θα επανέλθω
. [Πιθανώς ... θα επανέλθω dimplak έγραψε: ↑Παρ Απρ 24, 2020 10:24 amΕυχαριστώ για τις ιδέες σας. Θα τις επεξεργαστώ αναλυτικά.
Το χωρισμό λόγω συμμετρίας τον είχα σκεφτεί αλλά είχα φτάσει σε αδιέξοδα. Την αρχική σκέψη του κ. Κουτσουρίδη δεν την είχα σκεφτεί, δηλαδή
αν οι κορυφές παίζουν ρόλο στο πλήθος των ριζών.
Το άθροισμα των ριζών του κ. Παπαπέτρου μου έδωσε το ερέθισμα να πάρω τύπους Vieta για τηνκαι την
και να αποκλείσω περιπτώσεις αλλά δεν έχω καταλήξει κάπου.
 , το μεσαίο να είναι μηδέν και τα
, το μεσαίο να είναι μηδέν και τα Επειδή οι παραβολές είναι ορθογώνιες, τα τέσσερα σημεία τομής σχηματίζουν τετράπλευρο που είναι επίσης εγγράψιμο: σε σχετικά πρόσφατη συζήτηση είχα δώσει τύπους για το κέντρο του κύκλου (εδώ) και για την ακτίνα του (εδώ), εφαρμόζοντας τους στο συγκεκριμένο πρόβλημα βρίσκουμε κέντροAl.Koutsouridis έγραψε: ↑Πέμ Απρ 23, 2020 7:01 pmdimplak έγραψε: ↑Πέμ Απρ 23, 2020 6:45 pmΚαλησπέρα σας και ευχαριστώ για την άμεση ανταπόκριση.
Όσα προαναφέρατε τα έχω εξάγει και εγώ αλλά με προβληματίζει το γεγονός ότι και να βγάλουμε συνθήκη για τρία ακρότατα δε σημαίνει απαραίτητα
ότι έχει και 4 ρίζες η πολυωνυμική συνάρτηση 4ου βαθμού αλλά πιθανώς να έχει διότι το ακρότατο μπορεί να είναι θετικό αν η συνάρτηση φθίνει και μετά αυξάνει.
Προσπαθώ να προσανατολιστώ γεωμετρικά και με βάση ότι οι δύο παραβολές ανήκουν στην κατηγορία των ορθογώνιων παραβολών, δηλαδή
οι άξονες συμμετρίας τους είναι κάθετοι.
Γεωμετρικά ίσως βγουν πιο εύκολες σχέσεις για τοαν θεωρήσουμε, ότι εφόσον οι παραβολές τέμνονται σε τέσσερα σημεία, θα σχηματίζεται ένα περιγεγράψιμο παραβολικό τετράπλευρο. (βλέπε εδώ). Το κέντρο του εγγεγραμμένου κύκλου είναι σταθερό στην περίπτωσή μας, το σημείο
, που είναι το σημείο τομής των αξόνων των παραβολών. Αυτός ο κύκλος εφπάπτεται και στις δυο παραβολές. Οι εξισώσεις που προκύπτουν μπορεί να δίνουν τα κατάλληλα
. Δεν έχω κάνει τις πράξεις όμως, μπορεί να οδηγούν σε ισοδύναμα αποτελέσματα με την επίλυση των εξισώσεων, που δεν φαίνονται πολλά υποσχόμενες.
 ανεξάρτητο του
ανεξάρτητο του  και ακτίνα
και ακτίνα  -- δυστυχώς ο τύπος αυτός μας δίνει, μέσω μη αρνητικού υπόρριζου, την μη βέλτιστη συνθήκη
-- δυστυχώς ο τύπος αυτός μας δίνει, μέσω μη αρνητικού υπόρριζου, την μη βέλτιστη συνθήκη 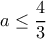 .
. και ακτίνα
και ακτίνα  ) για την οριακή περίπτωση
) για την οριακή περίπτωση  . Απλώς θα ήταν πολύ όμορφο να ορίζεται η ακτίνα αν και μόνον αν
. Απλώς θα ήταν πολύ όμορφο να ορίζεται η ακτίνα αν και μόνον αν  , αλλά ... ας μην τα θέλουμε και όλα δικά μας
, αλλά ... ας μην τα θέλουμε και όλα δικά μας 
 .
.dimplak έγραψε: ↑Πέμ Απρ 23, 2020 4:43 pmΝα βρείτε τις τιμές τουώστε οι παραβολές
και

να έχουν 4 σημεία τομής.
Γραφικά παρατηρούμε ότι αυτό συμβαίνει για. Δεν έχω καταφέρει να το αποδείξω αναλυτικά.
https://www.desmos.com/calculator/7n2kodqvjo
Οτι γιαChristos.N έγραψε: ↑Πέμ Απρ 23, 2020 6:35 pmμάλλον σαν διασταύρωση των ιδεών σου και όχι ως πλήρη λύση τα παρακάτω.
Καταλήγω στηνη οποία είναι τετάρτου βαθμού, για να έχει 4 πραγματικές ρίζες θα πρέπει η συνάρτηση
να παρουσιάζει τρία τοπικά ακρότατα (τ.ελ-τ.μεγ-τ.ελ) αντίστοιχα η πρώτη παράγωγος θα πρέπει να έχει τρεις πραγματικές ρίζες.
Όπουάρα μάλλον θα καταλήξουμε στην μελέτη-διερεύνηση της γνωστής πολυωνυμικής εξίσωσης 3ου βαθμού.
 υπάρχουν τέσσερα σημεία τομής είναι απλούστατο.
υπάρχουν τέσσερα σημεία τομής είναι απλούστατο.
 και τα όρια στα άπειρα είναι
και τα όρια στα άπειρα είναι 


 ,
,  και
και  . Η απόδειξη γίνεται εξετάζοντας την γωνία
. Η απόδειξη γίνεται εξετάζοντας την γωνία  , που για την κωνική
, που για την κωνική  είναι κοίλη και για την κωνική
είναι κοίλη και για την κωνική  είναι κυρτή, καταλλήγοντας σε άτοπο.
είναι κυρτή, καταλλήγοντας σε άτοπο.Το πρόβλημα βέβαια είναι ότι η παραπάνω πραγματική ρίζα,gbaloglou έγραψε: ↑Παρ Απρ 24, 2020 12:08 pmΉ ίσως θα μπορούσαμε να πάμε κατευθείαν στην γνωστή διερεύνηση λύσεων τεταρτοβάθμιας... Τέλος πάντων, δίνω μια 'γρήγορη' (αλλά όχι πλήρη) αιτιολόγηση για την 'οριακότητα' τηςChristos.N έγραψε: ↑Πέμ Απρ 23, 2020 6:35 pmμάλλον σαν διασταύρωση των ιδεών σου και όχι ως πλήρη λύση τα παρακάτω.
Καταλήγω στηνη οποία είναι τετάρτου βαθμού, για να έχει 4 πραγματικές ρίζες θα πρέπει η συνάρτηση
να παρουσιάζει τρία τοπικά ακρότατα (τ.ελ-τ.μεγ-τ.ελ) αντίστοιχα η πρώτη παράγωγος θα πρέπει να έχει τρεις πραγματικές ρίζες.
Όπουάρα μάλλον θα καταλήξουμε στην μελέτη-διερεύνηση της γνωστής πολυωνυμικής εξίσωσης 3ου βαθμού.
:
Αναζητούμε εκείνο τογια το οποίο η
θα έχει διπλή ρίζα, αναζητούμε δηλαδή
τέτοια ώστε να ισχύει η ισότητα
από την οποία εύκολα λαμβάνουμε
οπότε
και
Από τηνκαταλήγουμε εύκολα στην
, ενώ η πραγματική ρίζα της
οδηγεί, μέσω
&
και
, στις
,
. [Πιθανώς ... θα επανέλθω
]
 , καθιστά το παραπάνω υπόρριζο αρνητικό. Δεν έχω καλή εποπτεία της όλης κατάστασης, ας πώ όμως ότι η παραπάνω τιμή δίνει
, καθιστά το παραπάνω υπόρριζο αρνητικό. Δεν έχω καλή εποπτεία της όλης κατάστασης, ας πώ όμως ότι η παραπάνω τιμή δίνει  ... και δύο εφαπτόμενες παραβολές με ένα μόνο κοινό σημείο:
... και δύο εφαπτόμενες παραβολές με ένα μόνο κοινό σημείο:Λοιπόν ... επειδή πλήρης λύση τελικά δεν δόθηκε ... ας το τελειώσουμε χρησιμοποιώντας διακρίνουσες πολυωνύμου τετάρτου βαθμού:Christos.N έγραψε: ↑Πέμ Απρ 23, 2020 6:35 pmμάλλον σαν διασταύρωση των ιδεών σου και όχι ως πλήρη λύση τα παρακάτω.
Καταλήγω στηνη οποία είναι τετάρτου βαθμού, για να έχει 4 πραγματικές ρίζες θα πρέπει η συνάρτηση
να παρουσιάζει τρία τοπικά ακρότατα (τ.ελ-τ.μεγ-τ.ελ) αντίστοιχα η πρώτη παράγωγος θα πρέπει να έχει τρεις πραγματικές ρίζες.
Όπουάρα μάλλον θα καταλήξουμε στην μελέτη-διερεύνηση της γνωστής πολυωνυμικής εξίσωσης 3ου βαθμού.
 ,
,  ,
,  , ισοδύναμες αντίστοιχα προς τις
, ισοδύναμες αντίστοιχα προς τις


 , και ... επειδή η τριτοβάθμιος της τρίτης ανισότητας είναι προφανώς αρνητική για
, και ... επειδή η τριτοβάθμιος της τρίτης ανισότητας είναι προφανώς αρνητική για  ... φτάνουμε επιτέλους στην πολυπόθητη
... φτάνουμε επιτέλους στην πολυπόθητη  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες