Το τρίγωνο
 είναι ισόπλευρο και
είναι ισόπλευρο και  το μέσον της
το μέσον της  . Θεωρούμε το
. Θεωρούμε το  στην προέκταση της
στην προέκταση της 
και έστω
 η τομή της
η τομή της  με την ημιευθεία
με την ημιευθεία  . Το
. Το  είναι ορθογώνιο και ισοσκελές (Κατά KARKAR , ημιτετράγωνο!)
είναι ορθογώνιο και ισοσκελές (Κατά KARKAR , ημιτετράγωνο!)Αν ισχύει
 τότε να βρεθεί η γωνία
τότε να βρεθεί η γωνία  .Ευχαριστώ, Γιώργος.
.Ευχαριστώ, Γιώργος.Συντονιστής: gbaloglou
 είναι ισόπλευρο και
είναι ισόπλευρο και  το μέσον της
το μέσον της  . Θεωρούμε το
. Θεωρούμε το  στην προέκταση της
στην προέκταση της 
 η τομή της
η τομή της  με την ημιευθεία
με την ημιευθεία  . Το
. Το  είναι ορθογώνιο και ισοσκελές (Κατά KARKAR , ημιτετράγωνο!)
είναι ορθογώνιο και ισοσκελές (Κατά KARKAR , ημιτετράγωνο!) τότε να βρεθεί η γωνία
τότε να βρεθεί η γωνία  .Ευχαριστώ, Γιώργος.
.Ευχαριστώ, Γιώργος.Καλημέρα! ΈστωΓιώργος Μήτσιος έγραψε: ↑Δευ Φεβ 24, 2020 1:11 amΚαλημέρα.
Κι αυτή γνωστή γωνία.PNG
Το τρίγωνοείναι ισόπλευρο και
το μέσον της
. Θεωρούμε το
στην προέκταση της

και έστωη τομή της
με την ημιευθεία
. Το
είναι ορθογώνιο και ισοσκελές (Κατά KARKAR , ημιτετράγωνο!)
Αν ισχύειτότε να βρεθεί η γωνία
.Ευχαριστώ, Γιώργος.
 Από την υπόθεση,
Από την υπόθεση, 


 με διατέμνουσα
με διατέμνουσα 



 με διατέμνουσα
με διατέμνουσα 

 οπότε
οπότε 
 και
και 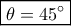
 έμεινε κατά λάθος στο σχήμα. Αγνοήστε το.
έμεινε κατά λάθος στο σχήμα. Αγνοήστε το.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες