Μία διαγώνιος, τέσσερις γωνίες
Συντονιστής: gbaloglou
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Μία διαγώνιος, τέσσερις γωνίες
Ξεκινώντας από απόπειρα επίλυσης άλλου προβλήματος (εδώ) προτείνω:
Να βρεθεί το μέγιστο και το ελάχιστο εμβαδόν -- ομοίως η μέγιστη και ελάχιστη περίμετρος -- τετραπλεύρου του οποίου γνωρίζουμε τις γωνίες και μία διαγώνιο.
[Μπορούν τα παραπάνω ερωτήματα να αναχθούν σε μελέτη συνάρτησης μιας κάποιας μεταβλητής, δεν φαίνεται όμως να υπάρχει 'καθαρή' λύση, το μέγιστο εμβαδόν για παράδειγμα μπορεί να εμφανίζεται είτε στα άκρα κάποιου διαστήματος ορισμού είτε σε εσωτερικό του σημείο. Ας το δει όποιος έχει κέφι να ασχοληθεί με κάτι τέτοιο, ελπίζω να παραθέσω σκέψεις και παραδείγματα αργότερα...]
Να βρεθεί το μέγιστο και το ελάχιστο εμβαδόν -- ομοίως η μέγιστη και ελάχιστη περίμετρος -- τετραπλεύρου του οποίου γνωρίζουμε τις γωνίες και μία διαγώνιο.
[Μπορούν τα παραπάνω ερωτήματα να αναχθούν σε μελέτη συνάρτησης μιας κάποιας μεταβλητής, δεν φαίνεται όμως να υπάρχει 'καθαρή' λύση, το μέγιστο εμβαδόν για παράδειγμα μπορεί να εμφανίζεται είτε στα άκρα κάποιου διαστήματος ορισμού είτε σε εσωτερικό του σημείο. Ας το δει όποιος έχει κέφι να ασχοληθεί με κάτι τέτοιο, ελπίζω να παραθέσω σκέψεις και παραδείγματα αργότερα...]
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Λέξεις Κλειδιά:
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μία διαγώνιος, τέσσερις γωνίες
Δίνω (μια κάποια) απάντηση για το εμβαδόν, αφήνοντας την περίμετρο για αργότερα:
Ξεκινάμε με (κυρτό) τετράπλευρο , όπου η διαγώνιος
, όπου η διαγώνιος  είναι σταθερή, έστω μήκους
είναι σταθερή, έστω μήκους  , το ίδιο και οι γωνίες
, το ίδιο και οι γωνίες  ,
,  ,
,  ,
,  . Θέτουμε
. Θέτουμε  ,
,  ,
,  ,
, 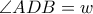 , έτσι ώστε
, έτσι ώστε  ,
,  ,
,  ,
,  , κλπ (Βλέπε και συνημμένο.)
, κλπ (Βλέπε και συνημμένο.)
Θεωρώντας τα κάθετα προς την ύψη των τριγώνων
ύψη των τριγώνων  και
και  και εφαρμόζοντας Νόμο Ημιτόνων υπολογίζουμε εύκολα τα εμβαδά τους και προσθέτοντας τα φτάνουμε εύκολα στην συνάρτηση-εμβαδόν για το
και εφαρμόζοντας Νόμο Ημιτόνων υπολογίζουμε εύκολα τα εμβαδά τους και προσθέτοντας τα φτάνουμε εύκολα στην συνάρτηση-εμβαδόν για το  :
:

όπου
ΜΑΧ{ ,
, }
} ΜΙΝ{
ΜΙΝ{ ,
, }.
}.
... Θα έλεγα ότι ο παραπάνω προσδιορισμός του πεδίου ορισμού απαιτεί περισσότερη προσοχή από τον προσδιορισμό της συνάρτησης! Έλεγξα τα αποτελέσματα μου κατά αρκετούς τρόπους (βλέπε και παραδείγματα στο συνημμένο), και πιστεύω ότι δεν υπάρχει λάθος. Πάντως δεν μπορώ να πω ότι έχω καλή εποπτεία του προβλήματος... Για παράδειγμα, δεν μου είναι εύκολο να πω πότε η συνάρτηση-εμβαδόν μεγιστοποιείται σε εσωτερικό σημείο του πεδίου ορισμού (μηδενισμός παραγώγου)* και πότε σε ένα από τα δύο άκρα του: δίνω κάποια παραδείγματα -- γράφημα συνάρτησης-εμβαδού για διάφορες τιμές (σε ακτίνια) των γωνιών ,
,  ,
,  και
και  -- στο συνημμένο, οι όποιες παρατηρήσεις ευπρόσδεκτες!
-- στο συνημμένο, οι όποιες παρατηρήσεις ευπρόσδεκτες!
* για εξέταση μηδενισμού παραγώγου μπορούμε να χρησιμοποιήσουμε και τον τύπο
![E(x)=\dfrac{d^2}{4}\left[\dfrac{cos\alpha-cos(2x+\alpha)}{sin\alpha}+\dfrac{cos\gamma-cos(2\beta+\gamma-2x)}{sin\gamma}\right]. E(x)=\dfrac{d^2}{4}\left[\dfrac{cos\alpha-cos(2x+\alpha)}{sin\alpha}+\dfrac{cos\gamma-cos(2\beta+\gamma-2x)}{sin\gamma}\right].](/forum/ext/geomar/texintegr/latexrender/pictures/186d5188783f355fb6b689f26bf2044d.png)
Ξεκινάμε με (κυρτό) τετράπλευρο
 , όπου η διαγώνιος
, όπου η διαγώνιος  είναι σταθερή, έστω μήκους
είναι σταθερή, έστω μήκους  , το ίδιο και οι γωνίες
, το ίδιο και οι γωνίες  ,
,  ,
,  ,
,  . Θέτουμε
. Θέτουμε  ,
,  ,
,  ,
, 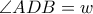 , έτσι ώστε
, έτσι ώστε  ,
,  ,
,  ,
,  , κλπ (Βλέπε και συνημμένο.)
, κλπ (Βλέπε και συνημμένο.)Θεωρώντας τα κάθετα προς την
 ύψη των τριγώνων
ύψη των τριγώνων  και
και  και εφαρμόζοντας Νόμο Ημιτόνων υπολογίζουμε εύκολα τα εμβαδά τους και προσθέτοντας τα φτάνουμε εύκολα στην συνάρτηση-εμβαδόν για το
και εφαρμόζοντας Νόμο Ημιτόνων υπολογίζουμε εύκολα τα εμβαδά τους και προσθέτοντας τα φτάνουμε εύκολα στην συνάρτηση-εμβαδόν για το  :
:
όπου
ΜΑΧ{
 ,
, }
} ΜΙΝ{
ΜΙΝ{ ,
, }.
}.... Θα έλεγα ότι ο παραπάνω προσδιορισμός του πεδίου ορισμού απαιτεί περισσότερη προσοχή από τον προσδιορισμό της συνάρτησης! Έλεγξα τα αποτελέσματα μου κατά αρκετούς τρόπους (βλέπε και παραδείγματα στο συνημμένο), και πιστεύω ότι δεν υπάρχει λάθος. Πάντως δεν μπορώ να πω ότι έχω καλή εποπτεία του προβλήματος... Για παράδειγμα, δεν μου είναι εύκολο να πω πότε η συνάρτηση-εμβαδόν μεγιστοποιείται σε εσωτερικό σημείο του πεδίου ορισμού (μηδενισμός παραγώγου)* και πότε σε ένα από τα δύο άκρα του: δίνω κάποια παραδείγματα -- γράφημα συνάρτησης-εμβαδού για διάφορες τιμές (σε ακτίνια) των γωνιών
 ,
,  ,
,  και
και  -- στο συνημμένο, οι όποιες παρατηρήσεις ευπρόσδεκτες!
-- στο συνημμένο, οι όποιες παρατηρήσεις ευπρόσδεκτες! * για εξέταση μηδενισμού παραγώγου μπορούμε να χρησιμοποιήσουμε και τον τύπο
![E(x)=\dfrac{d^2}{4}\left[\dfrac{cos\alpha-cos(2x+\alpha)}{sin\alpha}+\dfrac{cos\gamma-cos(2\beta+\gamma-2x)}{sin\gamma}\right]. E(x)=\dfrac{d^2}{4}\left[\dfrac{cos\alpha-cos(2x+\alpha)}{sin\alpha}+\dfrac{cos\gamma-cos(2\beta+\gamma-2x)}{sin\gamma}\right].](/forum/ext/geomar/texintegr/latexrender/pictures/186d5188783f355fb6b689f26bf2044d.png)
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μία διαγώνιος, τέσσερις γωνίες
Συνεχίζω (και τελειώνω) με την περίμετρο:
Χρησιμοποιώντας την ορολογία και μέθοδο της προηγούμενης δημοσίευσης, εκφράζουμε την περίμετρο ως
![\Pi(x)=d\left[\dfrac{sinx+sin(x+\alpha )}{sin\alpha }+\dfrac{sin(\beta -x)+sin(\beta +\gamma -x)}{sin\gamma}\right]= \Pi(x)=d\left[\dfrac{sinx+sin(x+\alpha )}{sin\alpha }+\dfrac{sin(\beta -x)+sin(\beta +\gamma -x)}{sin\gamma}\right]=](/forum/ext/geomar/texintegr/latexrender/pictures/43d37f8b616111157ee1dc6557d41f4e.png)
![=d\left[\dfrac{sin(x+\alpha /2)}{sin(\alpha /2)}+\dfrac{sin(\beta +\gamma /2-x)}{sin(\gamma /2)}\right], =d\left[\dfrac{sin(x+\alpha /2)}{sin(\alpha /2)}+\dfrac{sin(\beta +\gamma /2-x)}{sin(\gamma /2)}\right],](/forum/ext/geomar/texintegr/latexrender/pictures/23e2f6b407d9d1ef7d9ac02d3a28fb4a.png)
όπου ΜΑΧ{ ,
, }
} ΜΙΝ{
ΜΙΝ{ ,
, }.
}.
Σε θέματα μεγιστοποίησης και ελαχιστοποίησης, η περίμετρος συμπεριφέρεται ανάλογα με το εμβαδόν, οπότε δεν δίνω παραδείγματα όπως αυτά της προηγούμενης δημοσίευσης. Θα άξιζε ΙΣΩΣ τον κόπο, για όποιον έχει χρόνο και ενέργεια (και γνώση Geogebra), να μελετηθούν ειδικές περιπτώσεις όπως (εγγράψιμο τετράπλευρο),
(εγγράψιμο τετράπλευρο),  ,
,  . [Στην περίπτωση
. [Στην περίπτωση  προκύπτει εύκολα από τους τύπους ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για
προκύπτει εύκολα από τους τύπους ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για  , όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την δοθέντος μήκους διαγώνιο. Επίσης στην περίπτωση
, όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την δοθέντος μήκους διαγώνιο. Επίσης στην περίπτωση  προκύπτει ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για
προκύπτει ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για  , οπότε
, οπότε  και
και  , όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την μεσοκάθετο της δοθέντος μήκους διαγωνίου.]
, όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την μεσοκάθετο της δοθέντος μήκους διαγωνίου.]
Χρησιμοποιώντας την ορολογία και μέθοδο της προηγούμενης δημοσίευσης, εκφράζουμε την περίμετρο ως
![\Pi(x)=d\left[\dfrac{sinx+sin(x+\alpha )}{sin\alpha }+\dfrac{sin(\beta -x)+sin(\beta +\gamma -x)}{sin\gamma}\right]= \Pi(x)=d\left[\dfrac{sinx+sin(x+\alpha )}{sin\alpha }+\dfrac{sin(\beta -x)+sin(\beta +\gamma -x)}{sin\gamma}\right]=](/forum/ext/geomar/texintegr/latexrender/pictures/43d37f8b616111157ee1dc6557d41f4e.png)
![=d\left[\dfrac{sin(x+\alpha /2)}{sin(\alpha /2)}+\dfrac{sin(\beta +\gamma /2-x)}{sin(\gamma /2)}\right], =d\left[\dfrac{sin(x+\alpha /2)}{sin(\alpha /2)}+\dfrac{sin(\beta +\gamma /2-x)}{sin(\gamma /2)}\right],](/forum/ext/geomar/texintegr/latexrender/pictures/23e2f6b407d9d1ef7d9ac02d3a28fb4a.png)
όπου ΜΑΧ{
 ,
, }
} ΜΙΝ{
ΜΙΝ{ ,
, }.
}.Σε θέματα μεγιστοποίησης και ελαχιστοποίησης, η περίμετρος συμπεριφέρεται ανάλογα με το εμβαδόν, οπότε δεν δίνω παραδείγματα όπως αυτά της προηγούμενης δημοσίευσης. Θα άξιζε ΙΣΩΣ τον κόπο, για όποιον έχει χρόνο και ενέργεια (και γνώση Geogebra), να μελετηθούν ειδικές περιπτώσεις όπως
 (εγγράψιμο τετράπλευρο),
(εγγράψιμο τετράπλευρο),  ,
,  . [Στην περίπτωση
. [Στην περίπτωση  προκύπτει εύκολα από τους τύπους ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για
προκύπτει εύκολα από τους τύπους ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για  , όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την δοθέντος μήκους διαγώνιο. Επίσης στην περίπτωση
, όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την δοθέντος μήκους διαγώνιο. Επίσης στην περίπτωση  προκύπτει ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για
προκύπτει ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για  , οπότε
, οπότε  και
και  , όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την μεσοκάθετο της δοθέντος μήκους διαγωνίου.]
, όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την μεσοκάθετο της δοθέντος μήκους διαγωνίου.]Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μία διαγώνιος, τέσσερις γωνίες
gbaloglou έγραψε: ↑Σάβ Ιαν 18, 2020 1:42 pm[Στην περίπτωσηπροκύπτει εύκολα από τους τύπους ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για
, όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την δοθέντος μήκους διαγώνιο. Επίσης στην περίπτωση
προκύπτει ότι τόσο το εμβαδόν όσο και η περίμετρος μεγιστοποιούνται για
, οπότε
και
, όταν δηλαδή το τετράπλευρο είναι συμμετρικό περί την μεσοκάθετο της δοθέντος μήκους διαγωνίου.]
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
