 και η παραβολή :
και η παραβολή :  . Βρείτε τη μέγιστη
. Βρείτε τη μέγιστη τιμή του
 , για την οποία οι δύο καμπύλες έχουν ένα μόνο κοινό σημείο . Στην περίπτωση αυτή :
, για την οποία οι δύο καμπύλες έχουν ένα μόνο κοινό σημείο . Στην περίπτωση αυτή : Ευθεία διερχόμενη από το κέντρο
 του κύκλου , τέμνει την παραβολή στα σημεία
του κύκλου , τέμνει την παραβολή στα σημεία 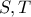
και τον κύκλο στα
 . Βρείτε το ελάχιστο του
. Βρείτε το ελάχιστο του  και το μέγιστο του
και το μέγιστο του 

 να έχει μοναδική λύση
να έχει μοναδική λύση στην αρχική παίρνουμε
στην αρχική παίρνουμε 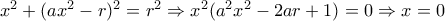 ή
ή  . Αν
. Αν  τότε έχουμε δύο λύσεις άρα
τότε έχουμε δύο λύσεις άρα  . Οπότε η μέγιστη τιμή του
. Οπότε η μέγιστη τιμή του 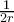
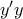 ):
):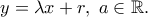
 στα σημεία που προκύπτουν από τη λύση του συστήματος:
στα σημεία που προκύπτουν από τη λύση του συστήματος:
 ):
):

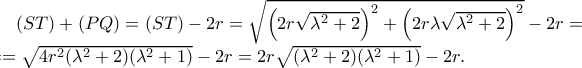
 , το οποίο, προφανώς, γίνεται ελάχιστο για
, το οποίο, προφανώς, γίνεται ελάχιστο για  , δηλαδή το ελάχιστο
, δηλαδή το ελάχιστο  .
.