Με πιο αγνά υλικά είναι η λύση του φίλου του Γιώργου του Βισβίκη . Έχω όμως και την κατασκευή.
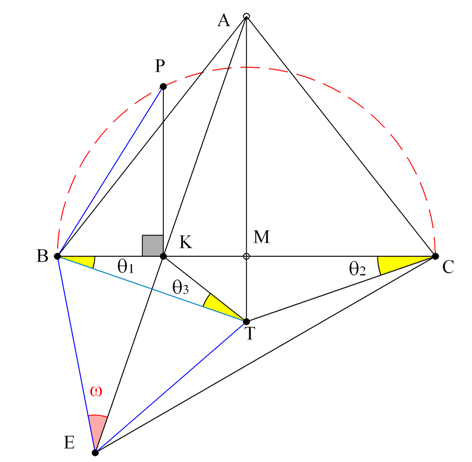
- Γωνία χωρίς εξαρτήσεις.png (33.55 KiB) Προβλήθηκε 600 φορές
Κατασκευή
Έστω

η διχοτόμος του

. Γράφω ημικύκλιο διαμέτρου

και τη κάθετο στην

στο

που το τέμνει στο

.
Επειδή

, γράφω τον κύκλο

που τέμνει τη προέκταση της

στο σημείο

. Λόγω της


.
Δηλαδή η

εφάπτεται του κύκλου

και άρα

.
Υπολογισμός γωνίας
Αν η κάθετη από το

στην

κόψει την

στο

, οι

είναι μεσοκάθετοι των

, άρα

Η προηγούμενη μας εξασφαλίζει ότι

εφάπτεται του κύκλου :

, οπότε:

που λόγω της

προκύπτει ότι το τρίγωνο

είναι ισόπλευρο και συνεπώς

.
 έχει
έχει  και
και  το μέσον της
το μέσον της  .
.  εντοπίζουμε το σημείο
εντοπίζουμε το σημείο  για το οποίο ισχύει
για το οποίο ισχύει 
 είναι σταθερή, ανεξάρτητη των γωνιών του
είναι σταθερή, ανεξάρτητη των γωνιών του 

 είναι
είναι 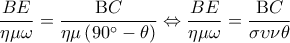 (1)
(1) είναι
είναι  (2)
(2) (3)
(3)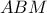 είναι
είναι  (4)
(4) , αφού είναι οξεία γωνία(*).
, αφού είναι οξεία γωνία(*). παρά στο
παρά στο  , άρα στο
, άρα στο  είναι
είναι  οπότε
οπότε 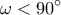 .
. που τέμνει την
που τέμνει την  στο
στο 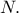 Προφανώς το
Προφανώς το  είναι χαρταετός και
είναι χαρταετός και 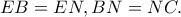 Είναι ακόμα,
Είναι ακόμα, 
 κι επειδή το
κι επειδή το  βρίσκεται στη μεσοκάθετο του
βρίσκεται στη μεσοκάθετο του  Άρα το
Άρα το  είναι ισόπλευρο και
είναι ισόπλευρο και 
 η διχοτόμος του
η διχοτόμος του  . Γράφω ημικύκλιο διαμέτρου
. Γράφω ημικύκλιο διαμέτρου  που το τέμνει στο
που το τέμνει στο  .
. , γράφω τον κύκλο
, γράφω τον κύκλο  που τέμνει τη προέκταση της
που τέμνει τη προέκταση της 
 .
. εφάπτεται του κύκλου
εφάπτεται του κύκλου  και άρα
και άρα  .
. , οι
, οι  είναι μεσοκάθετοι των
είναι μεσοκάθετοι των  , άρα
, άρα 
 εφάπτεται του κύκλου :
εφάπτεται του κύκλου :  , οπότε:
, οπότε: που λόγω της
που λόγω της  είναι ισόπλευρο και συνεπώς
είναι ισόπλευρο και συνεπώς  .
.