 , για την οποία είναι :
, για την οποία είναι :  .
.Β) Από σημείο
 της ακτίνας
της ακτίνας  , κύκλου διαμέτρου
, κύκλου διαμέτρου  , διέρχεται χορδή
, διέρχεται χορδή  κάθετη
κάθετη στη διάμετρο . Στην προέκταση της διαμέτρου θεωρούμε σημείο
 , ώστε :
, ώστε :  .
.Φέρουμε κάθετη στο
 προς την
προς την  την οποία η
την οποία η  , τέμνει στο
, τέμνει στο  .
.Σχηματίζω το παραλληλόγραμμο
 , του οποίου την πλευρά
, του οποίου την πλευρά  , η
, η  τέμνει στο
τέμνει στο  .
.Β1) Αν τα σημεία
 είναι συνευθειακά , δείξτε ότι :
είναι συνευθειακά , δείξτε ότι : 
Β2) Δείξτε ότι η γωνία
 , είναι η
, είναι η  του ερωτήματος
του ερωτήματος 
Β3) Δείξτε ότι :
 ...
... Υπάρχει ένα "θεματάκι" : Τα παραπάνω είναι ( προς το παρόν ) ... εικασίες

 και αφού
και αφού  , θα είναι
, θα είναι 
 ( το
( το  είναι παραλληλόγραμμο) ,
είναι παραλληλόγραμμο) ,  (εντός εκτός και επί τα αυτά των παραλλήλων
(εντός εκτός και επί τα αυτά των παραλλήλων 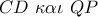 με τέμνουσα την
με τέμνουσα την  )
) ( το
( το  είναι ισοσκελές). Άρα
είναι ισοσκελές). Άρα  .Αν τώρα οι
.Αν τώρα οι 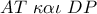 τέμνονται στο
τέμνονται στο  το τετράπλευρο
το τετράπλευρο  είναι ρόμβος .
είναι ρόμβος . και έτσι ,
και έτσι ,  .
. το τετράπλευρο
το τετράπλευρο  είναι ορθογώνιο οπότε:
είναι ορθογώνιο οπότε:  με άμεση συνέπεια το τετράπλευρο
με άμεση συνέπεια το τετράπλευρο  , είναι ισοσκελές τραπέζιο , άρα εγγράψιμο σε κύκλο . Αλλά και το
, είναι ισοσκελές τραπέζιο , άρα εγγράψιμο σε κύκλο . Αλλά και το  είναι εγγράψιμο
είναι εγγράψιμο  βλέπουν την
βλέπουν την  ανήκουν σε ένα κύκλο θα είναι
ανήκουν σε ένα κύκλο θα είναι 
 άρα
άρα 
 η
η  είναι διάμεσος του
είναι διάμεσος του  οπότε
οπότε 
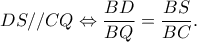 Αλλά το
Αλλά το  και με
και με 
 άρα η
άρα η  και τα
και τα  είναι συζυγή αρμονικά των
είναι συζυγή αρμονικά των 


 αλλά
αλλά  και
και  οπότε :
οπότε : 
 έχω
έχω 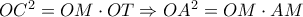
 χωρίζει το
χωρίζει το  σε μέσο κι άκρο λόγο .
σε μέσο κι άκρο λόγο .  είναι αρμονική και αφού
είναι αρμονική και αφού  τα
τα  χωρίζουν τα
χωρίζουν τα  σε μέσο κι άκρο λόγο.
σε μέσο κι άκρο λόγο.



 Αλλά,
Αλλά, 
 και
και 



 που ικανοποιεί το Α) ερώτημα.
που ικανοποιεί το Α) ερώτημα. )
)