Σελίδα 1 από 1
Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Σάβ Φεβ 09, 2019 12:36 pm
από george visvikis
Πιθανόν να έχει συζητηθεί ξανά. Στη
συλλογή ασκήσεων στο ισόπλευρο δεν την βρήκα (εκτός κι αν μου διέφυγε).
Το θέμα είναι ότι έχω λύση με Αναλυτική και ζητάω Ευκλείδεια λύση στην παρακάτω άσκηση:

- Μετρική σε ισόπλευρο.png (12.29 KiB) Προβλήθηκε 1226 φορές
Αν

είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου

πλευράς

, να υπολογίσετε το άθροισμα

Re: Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Σάβ Φεβ 09, 2019 2:53 pm
από Ορέστης Λιγνός
george visvikis έγραψε: ↑Σάβ Φεβ 09, 2019 12:36 pm
Πιθανόν να έχει συζητηθεί ξανά. Στη
συλλογή ασκήσεων στο ισόπλευρο δεν την βρήκα (εκτός κι αν μου διέφυγε).
Το θέμα είναι ότι έχω λύση με Αναλυτική και ζητάω Ευκλείδεια λύση στην παρακάτω άσκηση:
Μετρική σε ισόπλευρο.png
Αν

είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου

πλευράς

, να υπολογίσετε το άθροισμα

Καλησπέρα Γιώργο.
Από Πτολεμαίο, είναι

.
Έστω,

.
Είναι,

.
Τότε, από Ν. Συνημιτόνων στο

ή αλλιώς (*)

.
Όμως, είναι

. Η απόδειξη ολοκληρώθηκε.
(*) Αλλιώς, φέρνοντας

. Είναι,

.
Οπότε,
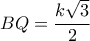
, και

. Με Π.Θ., είναι

.
Re: Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Σάβ Φεβ 09, 2019 6:47 pm
από george visvikis
Ορέστης Λιγνός έγραψε: ↑Σάβ Φεβ 09, 2019 2:53 pm
george visvikis έγραψε: ↑Σάβ Φεβ 09, 2019 12:36 pm
Πιθανόν να έχει συζητηθεί ξανά. Στη
συλλογή ασκήσεων στο ισόπλευρο δεν την βρήκα (εκτός κι αν μου διέφυγε).
Το θέμα είναι ότι έχω λύση με Αναλυτική και ζητάω Ευκλείδεια λύση στην παρακάτω άσκηση:
Μετρική σε ισόπλευρο.png
Αν

είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου

πλευράς

, να υπολογίσετε το άθροισμα

Καλησπέρα Γιώργο.
Από Πτολεμαίο, είναι

.
Έστω,

.
Είναι,

.
Τότε, από Ν. Συνημιτόνων στο

ή αλλιώς (*)

.
Όμως, είναι
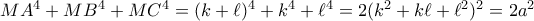
. Η απόδειξη ολοκληρώθηκε.
(*) Αλλιώς, φέρνοντας

. Είναι,

.
Οπότε,
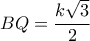
, και

. Με Π.Θ., είναι

.
Πολύ ωραία Ορέστη 
Re: Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Σάβ Φεβ 09, 2019 9:50 pm
από ΚΕΦΑΛΟΝΙΤΗΣ
Γιώργο , το θέμα έχει συζητηθεί στην παρακάτω δημοσίευση
https://www.mathematica.gr/forum/viewto ... BC#p215548
Xαίρομαι πολύ που ασχολήθηκε με το θέμα ο Ορέστης Λιγνός.
Ορέστη μου να είσαι πάντα καλά...
Re: Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Κυρ Φεβ 10, 2019 12:13 am
από george visvikis
Σ' ευχαριστώ Τηλέμαχε για την παραπομπή. Δεν το θυμόμουν καθόλου αν και είχα
συμμετάσχει σε ένα ερώτημα. Αν δεν δοθεί άλλη λύση, θα ανεβάσω μία με Αναλυτική.
Re: Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Κυρ Φεβ 10, 2019 9:38 am
από R BORIS
AN

μπορεί να αποδειχθεί ότι μόνο για
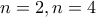
το

είναι σταθερό δηλαδή ανεξάρτητο του

H λύση με μιγαδικούς βρίσκεται στο βιβλίο μου Μιγαδικοί και μετ/μοί Moebius σελ 127 ασκηση Α11
Re: Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Κυρ Φεβ 10, 2019 1:16 pm
από STOPJOHN
george visvikis έγραψε: ↑Σάβ Φεβ 09, 2019 12:36 pm
Πιθανόν να έχει συζητηθεί ξανά. Στη
συλλογή ασκήσεων στο ισόπλευρο δεν την βρήκα (εκτός κι αν μου διέφυγε).
Το θέμα είναι ότι έχω λύση με Αναλυτική και ζητάω Ευκλείδεια λύση στην παρακάτω άσκηση:
Μετρική σε ισόπλευρο.png
Αν

είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου

πλευράς

, να υπολογίσετε το άθροισμα

Ειναι γνωστή η άσκηση

, θέτω

Oπότε θα υπολογισθεί

Για τα εμβαδά των τριγώνων

είναι

απο το θεώρημα της εσωτερικής διχοτόμου στο τρίγωνο

και

συνεπώς

Τα ορθογώνια τρίγωνα

είναι όμοια άρα

και λόγω της

Συνεπώς

Γιάννης
Re: Μετρική σε ισόπλευρο
Δημοσιεύτηκε: Δευ Φεβ 11, 2019 5:03 pm
από george visvikis
 είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου
είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου  πλευράς
πλευράς  , να υπολογίσετε το άθροισμα
, να υπολογίσετε το άθροισμα 
 είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου
είναι τυχαίο σημείο στον περίκυκλο ισοπλεύρου τριγώνου  πλευράς
πλευράς  , να υπολογίσετε το άθροισμα
, να υπολογίσετε το άθροισμα 
 .
. .
. .
. ή αλλιώς (*)
ή αλλιώς (*)  .
. . Η απόδειξη ολοκληρώθηκε.
. Η απόδειξη ολοκληρώθηκε. . Είναι,
. Είναι,  .
.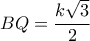 , και
, και  . Με Π.Θ., είναι
. Με Π.Θ., είναι  .
.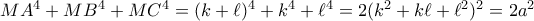 . Η απόδειξη ολοκληρώθηκε.
. Η απόδειξη ολοκληρώθηκε. μπορεί να αποδειχθεί ότι μόνο για
μπορεί να αποδειχθεί ότι μόνο για 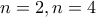 το
το  είναι σταθερό δηλαδή ανεξάρτητο του
είναι σταθερό δηλαδή ανεξάρτητο του  H λύση με μιγαδικούς βρίσκεται στο βιβλίο μου Μιγαδικοί και μετ/μοί Moebius σελ 127 ασκηση Α11
H λύση με μιγαδικούς βρίσκεται στο βιβλίο μου Μιγαδικοί και μετ/μοί Moebius σελ 127 ασκηση Α11 , θέτω
, θέτω 

 είναι
είναι 
 και
και  συνεπώς
συνεπώς 
 είναι όμοια άρα
είναι όμοια άρα  και λόγω της
και λόγω της 

 η πλευρά του ισοπλεύρου
η πλευρά του ισοπλεύρου  του οποίου οι συντεταγμένες των
του οποίου οι συντεταγμένες των  ένα τυχαίο σημείο του περιγεγραμμένου του κύκλου.
ένα τυχαίο σημείο του περιγεγραμμένου του κύκλου. 


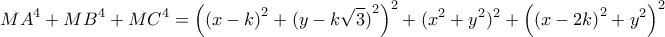
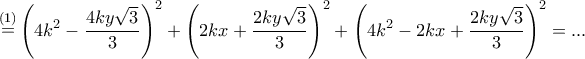

 θα είναι
θα είναι 