 , η πλευρά
, η πλευρά  παραμένει σταθερή ( ας πούμε
παραμένει σταθερή ( ας πούμε  ) ,
) , ενώ η
 μεταβάλλεται . Η διάμεσος
μεταβάλλεται . Η διάμεσος  τέμνει το ύψος
τέμνει το ύψος  στο σημείο
στο σημείο  .
.Υπολογίστε τη μέγιστη τιμή του τμήματος
 . Χρήση λογισμικού αποδεκτή .
. Χρήση λογισμικού αποδεκτή .Συντονιστής: gbaloglou
 , η πλευρά
, η πλευρά  παραμένει σταθερή ( ας πούμε
παραμένει σταθερή ( ας πούμε  ) ,
) ,  μεταβάλλεται . Η διάμεσος
μεταβάλλεται . Η διάμεσος  τέμνει το ύψος
τέμνει το ύψος  στο σημείο
στο σημείο  .
. . Χρήση λογισμικού αποδεκτή .
. Χρήση λογισμικού αποδεκτή . .
. ,
,  .
. και
και 
 .
. .
.Καλησπέρα. Δεν έγραψα ότι αυτό είναι το μέγιστο του
 . Έγραψα ότι το
. Έγραψα ότι το  παίρνει τη μέγιστη τιμή του όταν είναι περίπου
παίρνει τη μέγιστη τιμή του όταν είναι περίπου  .
.  που βρήκε ο Γιώργος Βισβίκης παραπάνω.
που βρήκε ο Γιώργος Βισβίκης παραπάνω.Ο κ. Ρίζος δεν έγραψε ότι το μέγιστο είναι
 αλλά ότι προσεγγιστικά έχει μέγιστο για
αλλά ότι προσεγγιστικά έχει μέγιστο για 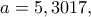 όπου
όπου  είναι η τεταγμένη του σημείου
είναι η τεταγμένη του σημείου  Με αντικατάσταση στον προηγούμενο τύπο, βρίσκεις τη μέγιστη τιμή.
Με αντικατάσταση στον προηγούμενο τύπο, βρίσκεις τη μέγιστη τιμή.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες