Ελάχιστη διάμεσος

#1

: Ελάχιστη διάμεσος.png (9.18 KiB) Προβλήθηκε 482 φορές

Στο τρίγωνο ABC

είναι $\widehat A=150^0$ και η διάμεσος

έχει σταθερό μήκος ίσο με

Να βρείτε συναρτήσει του

τη μικρότερη τιμή που μπορεί να πάρει η διάμεσος AM.

Altrian · #2

Κατασκευάζουμε τον κύκλο που διέρχεται από τα σημεία A,B,N

με κέντρο έστω

. Για κάθε σημείο έστω

του κύκλου
ισχύει ότι $\widehat{BKN}=180-150=30$ . Αρα η επίκεντρη $\widehat{BON}=60$ δηλαδή το $\triangle BON$ ισόπλευρο άρα η ακτίνα του κύκλου είναι

. Το σημείο

είναι σταθερό με BP=2PN

. Επομένως η ελάχιστη διάμεσος

συνεπάγεται και το ελάχιστο AP=(2/3*AM)

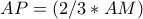. Το ζητούμενο σημείο

είναι το μοναδικό σημείο επαφής των κύκλων (O,d),(P,PA)

. Αρα

συνευθειακά και OA=d

.
Από π.θ. στο $\triangle OQP$ έχουμε $OP=d\frac{\sqrt{7}}{3}$ και $AP=d-OP=d (\frac{1-\sqrt{7}}{3})$
Τέλος
$min(AM)=3/2*min(AP)=d\left( \frac{3-\sqrt{7}}{2}\right)$

#3

george visvikis έγραψε: ↑
Παρ Αύγ 31, 2018 2:09 pm
Ελάχιστη διάμεσος.png
Στο τρίγωνο είναι $\widehat A=150^0$ και η διάμεσος έχει σταθερό μήκος ίσο με

Να βρείτε συναρτήσει του τη μικρότερη τιμή που μπορεί να πάρει η διάμεσος

Ανάλυση

: Ελάχιστη διάμεσος_1.png (29.12 KiB) Προβλήθηκε 399 φορές

Το σημείο

διατρέχει τα εσωτερικά σημεία σταθερού τόξου . Ας είναι

το σταθερό μέσο του

.

Επειδή η $\widehat {BAC} = \widehat {NME} = 150^\circ$ το σημείο

ανήκει σε σταθερό τόξο σταθερού κύκλου κέντρου

και μάλιστα το $\vartriangle KEN$ είναι σταθερό ισόπλευρο πλευράς $\dfrac{d}{2}$ .

Επίσης η

θα διέρχεται από το σταθερό βαρύκεντρο

του $\vartriangle ABC$ .

Επειδή $AM \geqslant KM - KA$ τη μικρότερη τιμή παίρνει όταν ισχύει το ίσον , δηλαδή όταν τα σημεία K,A,M

ανήκουν στην ίδια ευθεία.

Κατασκευή

: Ελάχιστη διάμεσος.png (27.72 KiB) Προβλήθηκε 399 φορές

Γράφω το σταθερό κύκλο κέντρου

. Φέρνω τη σταθερή

που τέμνει στο ${A_0}$ το σταθερό τόξο χορδής $BN\,\,$ που δέχεται γωνία $150^\circ$ .

Αν

το συμμετρικό του ${A_0}$ ως προς το

η

τέμνει την

στο

.

Επειδή , $GE \cdot GN = GM(GK + \dfrac{d}{2}) \Rightarrow \dfrac{d}{6} \cdot \dfrac{d}{3} = (KG - \dfrac{d}{2})(KG + \dfrac{d}{2})$

και άρα $KG = \dfrac{{d\sqrt 7 }}{6} \Rightarrow {A_0}M = 3GM = 3(\dfrac{d}{2} - \dfrac{{d\sqrt 7 }}{6}) \Rightarrow \boxed{{A_0}M = \dfrac{d}{2}(3 - \sqrt 7 )}$

S.E.Louridas · #4

Και μόνο για λόγους πλουραλισμού:

Θα θεωρήσουμε την διάμεσο

σταθερή και θα ζητήσουμε το μέγιστο d = BN

(σχήμα εισηγητή του θέματος), όταν η γωνία $\angle ATM$ είναι $\frac{\pi }{6},$ αν θεωρήσουμε το

ως το μέσον του NC.

Δηλαδή θέλουμε το μέγιστο του $MT = \frac{d}{2}.$ Όμως $OS = SK \Rightarrow M{T_{\max .}} = MS + ST = MS + SA.$
Έχουμε από το θ. διαμέσου: $3{R^2} + {R^2} = \frac{{{R^2}}}{2} + 2M{S^2} \Rightarrow ... \Rightarrow MS = \frac{{R\sqrt 7 }}{2},$
επομένως $M{T_{\max .}} = MS + SA = \frac{{R\left( {3 + \sqrt 7 } \right)}}{2} \Rightarrow$ $\frac{d}{2} = \frac{{R\left( {3 + \sqrt 7 } \right)}}{2} \Rightarrow R = \frac{{d\left( {3 - \sqrt 7 } \right)}}{2} \Rightarrow AM = \frac{{d\left( {3 - \sqrt 7 } \right)}}{2}.$

: διαμ.png (29.18 KiB) Προβλήθηκε 346 φορές

Ελάχιστη διάμεσος

Ελάχιστη διάμεσος

Re: Ελάχιστη διάμεσος

Re: Ελάχιστη διάμεσος

Re: Ελάχιστη διάμεσος

Μέλη σε σύνδεση