 και
και  . Το ορθογώνιο τρίγωνο
. Το ορθογώνιο τρίγωνο  , έχει την κορυφή
, έχει την κορυφή  της ορθής γωνίας στον μικρότερο κύκλο , τη
της ορθής γωνίας στον μικρότερο κύκλο , τη  στον μεσαίο
στον μεσαίοκαι την
 στον μεγάλο . Υπολογίστε το μέγιστο μήκος της υποτείνουσας
στον μεγάλο . Υπολογίστε το μέγιστο μήκος της υποτείνουσας  του τριγώνου .
του τριγώνου .Συντονιστής: gbaloglou
 και
και  . Το ορθογώνιο τρίγωνο
. Το ορθογώνιο τρίγωνο  , έχει την κορυφή
, έχει την κορυφή  της ορθής γωνίας στον μικρότερο κύκλο , τη
της ορθής γωνίας στον μικρότερο κύκλο , τη  στον μεσαίο
στον μεσαίο στον μεγάλο . Υπολογίστε το μέγιστο μήκος της υποτείνουσας
στον μεγάλο . Υπολογίστε το μέγιστο μήκος της υποτείνουσας  του τριγώνου .
του τριγώνου .Πιο βράδυ θα γράψω την αμιγώς γεωμετρική λύση πλήρως ( δεν είναι μεγάλης έκτασης)
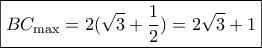
 το μέσο του
το μέσο του  και
και  το μέσο του
το μέσο του  .Από το α θεώρημα διαμέσων στα
.Από το α θεώρημα διαμέσων στα 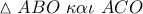 έχω:
έχω: 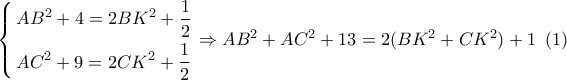 .
.  έχω :
έχω : 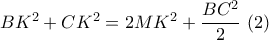
 δίδει
δίδει  δηλαδή το
δηλαδή το  διαγράφει το κύκλο
διαγράφει το κύκλο 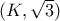 .
. προεκταθεί πέραν του
προεκταθεί πέραν του  και κόψει αυτόν τον κύκλο στο
και κόψει αυτόν τον κύκλο στο  , επειδή
, επειδή και αφού
και αφού 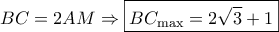
 ο κύκλος με διάμετρο την
ο κύκλος με διάμετρο την  και
και  το μέσο του
το μέσο του  . Ο κύκλος
. Ο κύκλος  τέμνει τον μοναδιαίο κύκλο εν γένει σε 2 σημεία. Μεγιστοποιείται δε (το μέγεθός του και άρα η ζητούμενη διάμετρός του) όταν τα σημεία αυτά ταυτίζονται (στο
τέμνει τον μοναδιαίο κύκλο εν γένει σε 2 σημεία. Μεγιστοποιείται δε (το μέγεθός του και άρα η ζητούμενη διάμετρός του) όταν τα σημεία αυτά ταυτίζονται (στο  ). Τότε ο μοναδιαίος κύκλος και ο κύκλος
). Τότε ο μοναδιαίος κύκλος και ο κύκλος  εφάπτονται εσωτερικά στο
εφάπτονται εσωτερικά στο  και επομένως τα σημεία
και επομένως τα σημεία 
 παίρνουμε:
παίρνουμε:
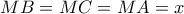 και επομένως
και επομένως  .
.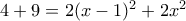

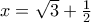 . Επομένως το ζητούμενο μέγιστο είναι
. Επομένως το ζητούμενο μέγιστο είναι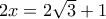
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 18 επισκέπτες