 οι
οι  έχουν σταθερά μήκη , (
έχουν σταθερά μήκη , (  και
και  ) , ενώ η βάση
) , ενώ η βάση  μεταβάλλεται .
μεταβάλλεται .Σχεδιάζουμε την τέμνουσα
 , με τα δεδομένα του σχήματος . Υπολογίστε το μέγιστο μέτρο της
, με τα δεδομένα του σχήματος . Υπολογίστε το μέγιστο μέτρο της  .
.Τροφή για μελέτη : Εξετάστε τη δυνατότητα λύσης στη γενική περίπτωση ...
Συντονιστής: gbaloglou
 οι
οι  έχουν σταθερά μήκη , (
έχουν σταθερά μήκη , (  και
και  ) , ενώ η βάση
) , ενώ η βάση  μεταβάλλεται .
μεταβάλλεται . , με τα δεδομένα του σχήματος . Υπολογίστε το μέγιστο μέτρο της
, με τα δεδομένα του σχήματος . Υπολογίστε το μέγιστο μέτρο της  .
.Καλημέρα Θανάση!KARKAR έγραψε:Στο τρίγωνοοι
έχουν σταθερά μήκη , (
και
) , ενώ η βάση
μεταβάλλεται .
Σχεδιάζουμε την τέμνουσα, με τα δεδομένα του σχήματος . Υπολογίστε το μέγιστο μέτρο της
.
Τροφή για μελέτη : Εξετάστε τη δυνατότητα λύσης στη γενική περίπτωση ...
 με διατέμνουσα
με διατέμνουσα  , ο Μενέλαος δίνει:
, ο Μενέλαος δίνει:  .
. και από τις αναλογίες προκύπτουν
και από τις αναλογίες προκύπτουν  . Αν λοιπόν
. Αν λοιπόν  , τότε
, τότε  και
και  .
. :
: 
 :
: 
 παρουσιάζει ελάχιστη τιμή για
παρουσιάζει ελάχιστη τιμή για  ίση με
ίση με 

 με διατέμνουσα
με διατέμνουσα  , δίνει
, δίνει 
 με διατέμνουσα
με διατέμνουσα  , δίνει
, δίνει  ,
, 
 , δίνει
, δίνει  (1)
(1) , δίνει
, δίνει  (2)
(2) και αντικαθιστώντας στην (1) , παίρνουμε :
και αντικαθιστώντας στην (1) , παίρνουμε : . Η συνάρτηση αυτή έχει παράγωγο
. Η συνάρτηση αυτή έχει παράγωγο 
 για
για  , οπότε
, οπότε  για
για  .
. , έγινε συμπτωματικά
, έγινε συμπτωματικάΣτο
 με διατέμνουσα
με διατέμνουσα  έχω :
έχω :  αν λοιπόν
αν λοιπόν  τότε
τότε 
 φέρνω τη διάμεσο
φέρνω τη διάμεσο  ( που είναι και ύψος) και τέμνει την
( που είναι και ύψος) και τέμνει την  στο
στο  . Στο
. Στο  επί την
επί την  φέρνω κάθετη που τέμνει την
φέρνω κάθετη που τέμνει την  στο
στο  .
. . Αλλά
. Αλλά  και άρα
και άρα  δηλαδή
δηλαδή  , έτσι αν
, έτσι αν  το
το 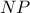 θα είναι :
θα είναι :  Μετά απ’ αυτά
Μετά απ’ αυτά  σχέσεις που μας εξασφαλίζουν ότι η
σχέσεις που μας εξασφαλίζουν ότι η  είναι αρμονική και επί πλέον στο
είναι αρμονική και επί πλέον στο  οι
οι  είναι εσωτερική και εξωτερική διχοτόμοι αντίστοιχα.
είναι εσωτερική και εξωτερική διχοτόμοι αντίστοιχα. επειδή
επειδή  δηλαδή η μεγαλύτερη τιμή του
δηλαδή η μεγαλύτερη τιμή του  είναι
είναι  κι αφού
κι αφού  οξεία θα έχει μεγίστη τιμή
οξεία θα έχει μεγίστη τιμή  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες