Προτείνω σε αυτό το νήμα να βάλουμε υπό μορφή ασκήσεων μερικούς χαρακτηρισμούς του βαρυκέντρου δηλαδή αν και μόνο αν συθήκες ώστε ένα σημείο να είναι βαρύκεντρο ενός τριγώνου.
Νομίζω ότι θα ήταν χρήσιμο για όλους ιδίως τους νέους συναδέλφους.
Αν κάτι παρόμοιο μας έχει απασχολήσει απολογούμαι.
Γράφω μερικούς πολύ γνωστούς που νομίζω μπορούμε να προσπεράσουμε:
1) Το
 είναι βαρύκεντρο του
είναι βαρύκεντρο του  αν και μόνο αν ανήκει σε δύο διαμέσους του.
αν και μόνο αν ανήκει σε δύο διαμέσους του. 2) Το
 είναι βαρύκεντρο του
είναι βαρύκεντρο του  αν και μόνο αν ανήκει σε μία διάμεσο και απέχει από την κορυφή διπλάσια απόσταση απ' ότι από το μέσο της απέναντι πλευράς.
αν και μόνο αν ανήκει σε μία διάμεσο και απέχει από την κορυφή διπλάσια απόσταση απ' ότι από το μέσο της απέναντι πλευράς. 3) Το
 είναι βαρύκεντρο του
είναι βαρύκεντρο του  αν και μόνο αν
αν και μόνο αν  .
.4) Το
 είναι βαρύκεντρο του
είναι βαρύκεντρο του  αν και μόνο αν οι συντεταγμένες του είναι οι αριθμητικοί μέσοι των συντεταγμένων των κορυφών δηλαδή
αν και μόνο αν οι συντεταγμένες του είναι οι αριθμητικοί μέσοι των συντεταγμένων των κορυφών δηλαδή  .
.5) Το
 είναι βαρύκεντρο του
είναι βαρύκεντρο του  αν και μόνο αν
αν και μόνο αν 

 όπου
όπου  και
και  το περίκεντρο και το ορθόκεντρο του τριγώνου αντίστοιχα. (δηλαδή το
το περίκεντρο και το ορθόκεντρο του τριγώνου αντίστοιχα. (δηλαδή το  τότε ισχύει
τότε ισχύει 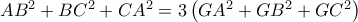 . Δε γνώριζα λοιπόν ότι ισχύει και το αντίστροφο και χρειάστηκε προηγουμένως να το αποδείξω. Συνεπώς:
. Δε γνώριζα λοιπόν ότι ισχύει και το αντίστροφο και χρειάστηκε προηγουμένως να το αποδείξω. Συνεπώς: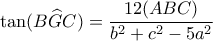 (Βέβαια απαιτεί απόδειξη).
(Βέβαια απαιτεί απόδειξη). το μέσο τηςν
το μέσο τηςν  ,
,  οποιοδήποτε σημείο του επιπέδου και
οποιοδήποτε σημείο του επιπέδου και  η απόσταση του
η απόσταση του 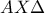 έχουμε
έχουμε

 έχουμε:
έχουμε:
 βρίσκουμε ότι:
βρίσκουμε ότι:

 κυκλικά και προσθέτοντας έχουμε:
κυκλικά και προσθέτοντας έχουμε:

 δηλαδή του
δηλαδή του  έχει πλευρές
έχει πλευρές  . Αν ονομάσουμε για λόγους συντομίας
. Αν ονομάσουμε για λόγους συντομίας  από τον νόμο των συνημιτόνων έχουμε
από τον νόμο των συνημιτόνων έχουμε 
 .
.

 μπορούμε να κατασκευάσουμε άπειρα τρίγωνα με την
μπορούμε να κατασκευάσουμε άπειρα τρίγωνα με την  να είναι ορθή ή ισοδύναμα
να είναι ορθή ή ισοδύναμα  ). Θα μπορούσαμε να καλύψουμε και αυτή την ειδική αυτή περίπτωση αν αντί της εφαπτομένης πάρουμε το ημίτονο. Αν οι υπολογισμοί μου είναι σωστoί η συνθήκη, που είναι αρκετά φορτωμένη, θα είναι
). Θα μπορούσαμε να καλύψουμε και αυτή την ειδική αυτή περίπτωση αν αντί της εφαπτομένης πάρουμε το ημίτονο. Αν οι υπολογισμοί μου είναι σωστoί η συνθήκη, που είναι αρκετά φορτωμένη, θα είναι .
.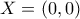 . Έστω
. Έστω  και
και  . Τότε
. Τότε  .
. . Το δεξί μέλος ισούται με
. Το δεξί μέλος ισούται με
 είναι βαρύκεντρο του τριγώνου
είναι βαρύκεντρο του τριγώνου  ,
,  ,
,  τέμνουν τις
τέμνουν τις  ,
,  ,
,  στα
στα  ,
,  ,
,  έτσι ώστε
έτσι ώστε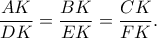
 , τότε
, τότε 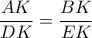 μας δίνει ότι τα τρίγωνα
μας δίνει ότι τα τρίγωνα 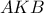 και
και  είναι όμοια. Άρα
είναι όμοια. Άρα  και οι
και οι  είναι παράλληλες. Άρα
είναι παράλληλες. Άρα  οπότε από Ceva παίρνουμε
οπότε από Ceva παίρνουμε  . Δηλαδή η
. Δηλαδή η  είναι διάμεσος. Ομοίως και οι
είναι διάμεσος. Ομοίως και οι  είναι διάμεσοι οπότε το
είναι διάμεσοι οπότε το  Τότε από Ceva είναι
Τότε από Ceva είναι  Αλλά από Van Aubel, η δοσμένη
Αλλά από Van Aubel, η δοσμένη  και επειδή
και επειδή  εύκολα προκύπτει ότι
εύκολα προκύπτει ότι 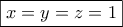
 είναι διάμεσοι του τριγώνου.
είναι διάμεσοι του τριγώνου. στο
στο 



 από την
από την  και την προτελευταία σχέση έχει απο μόνη της ενδιαφέρον σαν αυττελής άσκηση Άλγεβρας.
και την προτελευταία σχέση έχει απο μόνη της ενδιαφέρον σαν αυττελής άσκηση Άλγεβρας.

 οπότε από
οπότε από 
 άρα και
άρα και 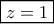
 που αφήνει τα
που αφήνει τα  προς το ίδιο μέρος του επιπέδου η μέση τιμή των αποστάσεων των
προς το ίδιο μέρος του επιπέδου η μέση τιμή των αποστάσεων των ,
,  τις κορυφές του τριγώνου.
τις κορυφές του τριγώνου. τυχούσα ευθεία που έχει τις πλευρές του τριγώνου προς το αυτό μέρος της. Τότε και το βαρύκεντρο βρίσκεται προς τι ίδιο μέρος της ευθείας. Μπορούμε να υποθέσουμε χωρίς να βλάπτεται η γενικότητα ότι
τυχούσα ευθεία που έχει τις πλευρές του τριγώνου προς το αυτό μέρος της. Τότε και το βαρύκεντρο βρίσκεται προς τι ίδιο μέρος της ευθείας. Μπορούμε να υποθέσουμε χωρίς να βλάπτεται η γενικότητα ότι  διαφορετικά διαιρούμε την εξίσωση της ευθείας μς
διαφορετικά διαιρούμε την εξίσωση της ευθείας μς  και ότι
και ότι 
 που έχει την δοθείσα ιδιότητα. Έστω
που έχει την δοθείσα ιδιότητα. Έστω 

 .
. με
με  . Αν υποτεθεί ότι
. Αν υποτεθεί ότι 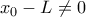 τότε
τότε  και
και  που μας οδηγεί στο άτοπο συμπέρασμα ότι το
που μας οδηγεί στο άτοπο συμπέρασμα ότι το  μπορεί να πάρει το πολύ δύο τιμές. Άρα
μπορεί να πάρει το πολύ δύο τιμές. Άρα  . Όμοια
. Όμοια  και επομέως το
και επομέως το  του τριγώνου
του τριγώνου  , όπου
, όπου  και
και  . Τότε:
. Τότε: αν και μόνον αν ισχύει
αν και μόνον αν ισχύει 

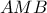 με τέμνουσα
με τέμνουσα  απο Θ. Μενελάου
απο Θ. Μενελάου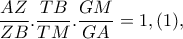 Ομοίως στο τρίγωνο
Ομοίως στο τρίγωνο  με
με 



 διάμεσος στο τραπέζιο
διάμεσος στο τραπέζιο  )
)