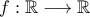 που ικανοποιούν την συναρτησιακή σχέση
που ικανοποιούν την συναρτησιακή σχέση 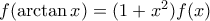 για κάθε
για κάθε  .
.Συντονιστής: emouroukos
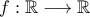 που ικανοποιούν την συναρτησιακή σχέση
που ικανοποιούν την συναρτησιακή σχέση 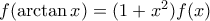 για κάθε
για κάθε  .
. με τύπο
με τύπο
 . Επίσης, ορίζοντας
. Επίσης, ορίζοντας  έχουμε
έχουμε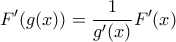
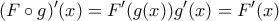
 για κάποιο
για κάποιο  . Για
. Για  παίρνουμε
παίρνουμε  άρα
άρα 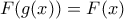 για κάθε
για κάθε  .
.  ορίζω την ακολουθία
ορίζω την ακολουθία  με
με  και
και  για
για  . Η
. Η  είναι φθίνουσα ακολουθία θετικών όρων άρα συγκλίνει σε κάποιο όριο
είναι φθίνουσα ακολουθία θετικών όρων άρα συγκλίνει σε κάποιο όριο 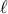 για το οποίο ισχύει
για το οποίο ισχύει 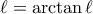 . Άρα η
. Άρα η  συγκλίνει στο
συγκλίνει στο  . Όμως
. Όμως 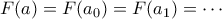 και από τη συνέχεια της
και από τη συνέχεια της  έχουμε
έχουμε 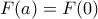 . Ομοίως και
. Ομοίως και 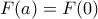 αν
αν  .
. είναι σταθερή και άρα η
είναι σταθερή και άρα η  είναι η μηδενική συνάρτηση.
είναι η μηδενική συνάρτηση.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 28 επισκέπτες