Έστω
![f:[0,1]->[0,1] f:[0,1]->[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/854192dcb00d4327ab798ad57e0ecae3.png) με
με 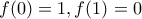 , γνησίως φθίνουσα, συνεχής, και
, γνησίως φθίνουσα, συνεχής, και  για κάθε
για κάθε ![x\in[0,1] x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ee73e01397b466fca4731317471bd6ff.png) . Να δείξετε ότι υπάρχει γνησίως αύξουσα συνεχής
. Να δείξετε ότι υπάρχει γνησίως αύξουσα συνεχής ![g:[0,1]->\mathbb{R} g:[0,1]->\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/5698a9e0029dbdfd752b0ac5eae676cd.png) με
με  τέτοια ώστε
τέτοια ώστε 
Συντονιστής: emouroukos
![f:[0,1]->[0,1] f:[0,1]->[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/854192dcb00d4327ab798ad57e0ecae3.png) με
με 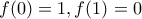 , γνησίως φθίνουσα, συνεχής, και
, γνησίως φθίνουσα, συνεχής, και  για κάθε
για κάθε ![x\in[0,1] x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ee73e01397b466fca4731317471bd6ff.png) . Να δείξετε ότι υπάρχει γνησίως αύξουσα συνεχής
. Να δείξετε ότι υπάρχει γνησίως αύξουσα συνεχής ![g:[0,1]->\mathbb{R} g:[0,1]->\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/5698a9e0029dbdfd752b0ac5eae676cd.png) με
με  τέτοια ώστε
τέτοια ώστε 
Υπάρχει μοναδικό
 με
με  .
.![\displaystyle g:[0,x_0]\rightarrow \mathbb{R} \displaystyle g:[0,x_0]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/c25b356ab1806858620c200ace552ece.png) γνησίως αύξουσα με
γνησίως αύξουσα με  .
. θέτουμε
θέτουμε
![[x_0,1] [x_0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5aa4a519bb7b340c2ab716e6c220fd59.png) η
η  είναι συνεχής και γνησίως αύξουσα.
είναι συνεχής και γνησίως αύξουσα. .
.
![[x_0,1] [x_0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5aa4a519bb7b340c2ab716e6c220fd59.png)
 θέτουμε
θέτουμε  όπου
όπου  .
.
 (λόγω της
(λόγω της  )
)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες