Ένα ενδιαφέρον θέμα το οποίο μπορεί να "γεννήσει" ενδιαφέρουσες ασκήσεις:
Δίνονται οι συναρτήσεις
 και
και  με
με  . (Στην ουσία πρόκειται για τη συνάρτηση
. (Στην ουσία πρόκειται για τη συνάρτηση  αλλά την έγραψα έτσι για να είναι εντός ύλης της Γ Λυκείου όπου οι μόνες λογαριθμικές που επιτρέπεται να εμφανίζονται είναι οι
αλλά την έγραψα έτσι για να είναι εντός ύλης της Γ Λυκείου όπου οι μόνες λογαριθμικές που επιτρέπεται να εμφανίζονται είναι οι  και
και  ).
). Να βρείτε την τιμή
Να βρείτε την τιμή 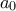 του
του  , ώστε οι δύο αυτές συναρτήσεις να έχουν μοναδικό σημείο τομής.
, ώστε οι δύο αυτές συναρτήσεις να έχουν μοναδικό σημείο τομής. Να δείξετε ότι για
Να δείξετε ότι για  δεν έχουν κοινά σημεία, ενώ για
δεν έχουν κοινά σημεία, ενώ για  έχουν ακριβώς
έχουν ακριβώς  κοινά σημεία τομής.
κοινά σημεία τομής.Σχόλιο: Γνωρίζουμε ότι το γνωστό ζεύγος συναρτήσεων
 και
και  δεν έχει κοινά σημεία (η απόξειξη μπορεί να γίνει με ποικίλους τρόπους). Στην ουσία το παραπάνω θέμα, βρίσκει το "κατάλληλο" ζεύγος εκθετικής-λογαριθμικής συνάρτησης το οποίο είναι τέτοιο ώστε οι δύο συναρτήσεις να τέμνονται σε ένα και μόνο σημείο και οποιοδήποτε άλλο ζεύγος να έχει είτε ακριβώς
δεν έχει κοινά σημεία (η απόξειξη μπορεί να γίνει με ποικίλους τρόπους). Στην ουσία το παραπάνω θέμα, βρίσκει το "κατάλληλο" ζεύγος εκθετικής-λογαριθμικής συνάρτησης το οποίο είναι τέτοιο ώστε οι δύο συναρτήσεις να τέμνονται σε ένα και μόνο σημείο και οποιοδήποτε άλλο ζεύγος να έχει είτε ακριβώς  σημεία τομής είτε κανένα.
σημεία τομής είτε κανένα.
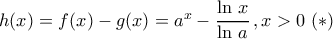 . Όπως γνωρίζουμε η
. Όπως γνωρίζουμε η  είναι γνησίως αύξουσα
είναι γνησίως αύξουσα  με σύνολο τιμών
με σύνολο τιμών  . Επομένως, ορίζεται η
. Επομένως, ορίζεται η  και έχουμε ότι για δοθέν
και έχουμε ότι για δοθέν η εξίσωση
η εξίσωση  έχει λύση ως προς
έχει λύση ως προς  την
την  . Συνεπώς,
. Συνεπώς,  και εφ' όσον η
και εφ' όσον η  ισοδυναμεί με την
ισοδυναμεί με την 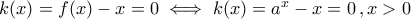 . Παραγωγίζουμε και ισχύει
. Παραγωγίζουμε και ισχύει  . Σε όλο το
. Σε όλο το  έχει μοναδική λύση
έχει μοναδική λύση 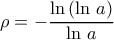
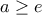 ισχύει
ισχύει  και άρα η
και άρα η  διατηρεί πρόσημο. Επειδή,
διατηρεί πρόσημο. Επειδή,  και
και  έπεται
έπεται  γνησίως αύξουσα χωρίς ρίζα στο
γνησίως αύξουσα χωρίς ρίζα στο  για το οποίο
για το οποίο  και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  όπου
όπου ![\displaystyle{k(\left(0,+\infty\right))=\left[k(\rho),k(0)\right)\cup\left[k(\rho),\lim_{x\to +\infty}f(x)\right]=\left[\dfrac{1+\ln\,(\ln\,a)}{\ln\,a},1\right)\cup\left[\dfrac{1+\ln\,(\ln\,a)}{\ln\,a},+\infty\right)} \displaystyle{k(\left(0,+\infty\right))=\left[k(\rho),k(0)\right)\cup\left[k(\rho),\lim_{x\to +\infty}f(x)\right]=\left[\dfrac{1+\ln\,(\ln\,a)}{\ln\,a},1\right)\cup\left[\dfrac{1+\ln\,(\ln\,a)}{\ln\,a},+\infty\right)}](/forum/ext/geomar/texintegr/latexrender/pictures/0de0acb228e25b2cd032ed803eaee16f.png)
 διότι
διότι 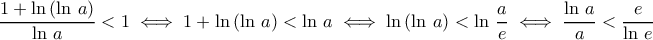 (που ισχύει για
(που ισχύει για  ).
). (και μάλιστα
(και μάλιστα  ) και για
) και για  θα έχουμε 2 ακριβώς ρίζες, μια στο
θα έχουμε 2 ακριβώς ρίζες, μια στο  ενώ για
ενώ για  δεν τέμνονται. Τελική απάντηση
δεν τέμνονται. Τελική απάντηση  .
. τότε
τότε 

 για κάποιο
για κάποιο  kαι ας είναι πχ
kαι ας είναι πχ τότε
τότε  αντιφαση
αντιφαση Nα βρείτε τον τυπο της
Nα βρείτε τον τυπο της 
 ώστε η γραφική παράσταση της
ώστε η γραφική παράσταση της  να εφάπτεται στην ευθεία
να εφάπτεται στην ευθεία  . Προφανώς τότε, το σημείο επαφής θα είναι ταυτόχρονα και το σημείο επαφής με την γραφική παράσταση της
. Προφανώς τότε, το σημείο επαφής θα είναι ταυτόχρονα και το σημείο επαφής με την γραφική παράσταση της  το οποίο και θα είναι το μοναδικό κοινό σημείο των δύο συναρτήσεων.
το οποίο και θα είναι το μοναδικό κοινό σημείο των δύο συναρτήσεων. .
. έχουμε
έχουμε  , ενώ για
, ενώ για  αποδεικνύεται ότι η
αποδεικνύεται ότι η  τέμνει την
τέμνει την